Brillouin zone
From Online Dictionary of Crystallography
(Redirected from Brillouin zones)
Zone de Brillouin (Fr). Brillouin-Zone (Ge). Zona di Brillouin (It). ブリュアンゾーン (Ja). Zona de Brillouin (Sp).
Definition
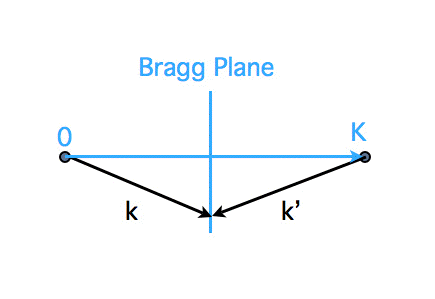
A Brillouin zone is a particular choice of the unit cell of the reciprocal lattice. It is defined as the Wigner-Seitz cell (also called Dirichlet or Voronoi domain of influence) of the reciprocal lattice. It is constructed as the set of points enclosed by the Bragg planes, the planes perpendicular to a connection line from the origin to each lattice point and passing through the midpoint (see figure). Alternatively, it is defined as the set of points closer to the origin than to any other reciprocal lattice point. The whole reciprocal space may be covered without overlap with copies of such a Brillouin zone.
For high-symmetry lattices one introduces sometimes the notion of n-th Brillouin Zone. This is the set of points one reaches with a straight line from the origin and passing through n-1 Bragg planes. In this terminology, the Brillouin zone defined above is the first Brillouin zone. The n-th Brillouin zone is a shell around lower Brillouin zones and its shape becomes for higher values of n rapidly rather complicated (see figure).
Vectors in the Brillouin zone or on its boundary characterize states in a system with lattice periodicity, e.g. phonon or electron states. States are non-equivalent if they belong to different vectors in a unit cell of the reciprocal lattice. This is not necessarily the Brillouin zone. Especially, for low-symmetry systems Brillouin zones are sometimes difficult to visualize, and another choice of unit cell may be useful, e.g. the parallelepiped spanned by the basis vectors.
The Brillouin zone boundary consists of pieces of Bragg planes. Since two points on the boundary may differ by a reciprocal lattice vector, only a part of the boundary may be used for characterization of states. There is no simple rule for that choice. Dispersion curves at the zone boundary have either a maximum or minimum there or they merge with other curves giving rise to a change of degeneracy.
See also
- Domain of influence
- Sayre, D. (1952). Acta Cryst. 5, 60-65. The squaring method: a new method for phase determination.
- Chapter 2.2 of International Tables for Crystallography, Volume D