Difference between revisions of "Miller indices"
From Online Dictionary of Crystallography
(→History: merging the example page) |
BrianMcMahon (talk | contribs) m |
||
| Line 57: | Line 57: | ||
</table> | </table> | ||
| − | ==Example== | + | == Example == |
<center> | <center> | ||
'''Orientation of lattice planes depending on their Miller indices''' | '''Orientation of lattice planes depending on their Miller indices''' | ||
| Line 65: | Line 65: | ||
The Miller indices of the planes <font color="green">''ABC' '' </font>, <font color="red">''ABC''</font>, <font color="blue">''ABC" ''</font>, <font color="purple"> ''AA"BB" '' </font> are <font color="green">(112) </font>, <font color="red">(111)</font>, <font color="blue">(221)</font>, <font color="purple"> (110)</font>, respectively. These planes have <font color="green">''AB'' </font>, or <math> [1{\bar 1}0]</math>, as common zone axis. | The Miller indices of the planes <font color="green">''ABC' '' </font>, <font color="red">''ABC''</font>, <font color="blue">''ABC" ''</font>, <font color="purple"> ''AA"BB" '' </font> are <font color="green">(112) </font>, <font color="red">(111)</font>, <font color="blue">(221)</font>, <font color="purple"> (110)</font>, respectively. These planes have <font color="green">''AB'' </font>, or <math> [1{\bar 1}0]</math>, as common zone axis. | ||
| − | |||
== History == | == History == | ||
| Line 75: | Line 74: | ||
[[law of rational indices]]<br> | [[law of rational indices]]<br> | ||
[[reciprocal lattice]] | [[reciprocal lattice]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
[[Category:Fundamental crystallography]]<br> | [[Category:Fundamental crystallography]]<br> | ||
Revision as of 16:53, 6 February 2012
Indices de Miller (Fr.). Indices de Miller (Sp). Indici di Miller (It). ミラー指数 (Ja)
Contents
[hide]Definition
Direct space
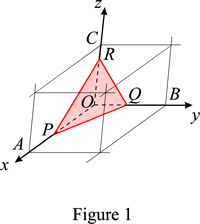
Planes of a given family of lattice planes with Miller indices h, k, l make intercepts OP = C a/h, OQ = C b/k, and OR = C c/l with the unit-cell axes OA = a, OB = b, and OC = c (see Figure 1), where h, k, l are prime integers and C is a constant integer; the planes of the family are denoted (hkl). This property results from the law of rational indices. The Miller indices of the equivalent faces of a crystal form are denoted by {hkl}. The variation of the orientation of the planes with the ratios of the Miller indices is illustrated in the attached examples. The equation of the planes of the family is:
hx + ky + lz = C
Reciprocal space
The reciprocal lattice vector associated to the family of lattice planes is OH = h a* + k b* + l c*, where a*, b*, c* are the reciprocal lattice basis vectors. OH is perpendicular to the family of lattice planes and OH = 1/d where d is the lattice spacing of the family.
Bravais-Miller indices (hexagonal axes)
In the case of an hexagonal lattice, one uses four axes, a1, a2, a3, c and four indices, (hkil), called Bravais-Miller indices, where h, k, i, l are again inversely proportional to the intercepts of a plane of the family with the four axes. The indices h, k, i are cyclically permutable and are related by
h + k + i = 0
Behaviour in a change of basis
In a change of basis the Miller indices h, k, l transform like the basis vectors a, b, c and are for that reason covariant quantities.
Rhombohedral crystals
The Miller indices hR, kR, lR referred to rhombohedral axes are related to the corresponding indices, hH, kH, iH,lH reffered to hexagonal axes by:
| hH = kR - lR | ; | hR = ⅓(- kH + iH + lH) |
| kH = lR - hR | ; | kR = ⅓(hH - iH + lH) |
| iH = hR - kR | ; | lR = ⅓(- hH + kH + lH) |
| lH = hR + kR + lR |
Example
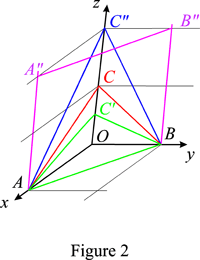
Orientation of lattice planes depending on their Miller indices
The Miller indices of the planes ABC' , ABC, ABC" , AA"BB" are (112) , (111), (221), (110), respectively. These planes have AB , or [1{\bar 1}0], as common zone axis.
History
The Miller indices were first introduced, among others, by W. Whewell in 1829 and developed by W.H. Miller, his successor at the Chair of Mineralogy at Cambridge University, in his book A treatise on Crystallography (1839) - see Historical Atlas of Crystallography (1990), edited by J. Lima de Faria, published for the International Union of Crystallography by Kluwer Academic Publishers, Dordrecht.