Difference between revisions of "Modulated crystal structure"
From Online Dictionary of Crystallography
m (titles level) |
BrianMcMahon (talk | contribs) m |
||
| Line 1: | Line 1: | ||
<Font color="blue">Structure cristalline modulée</font> (Fr.), <Font color="black"> Struttura cristallina modulata </Font>(''It''), <Font color="purple"> 変調構造 </Font>(''Ja'') | <Font color="blue">Structure cristalline modulée</font> (Fr.), <Font color="black"> Struttura cristallina modulata </Font>(''It''), <Font color="purple"> 変調構造 </Font>(''Ja'') | ||
| − | ==Definition== | + | == Definition == |
A ''modulated crystal structure'' is a density (or atom arrangement) that may be obtained from a density | A ''modulated crystal structure'' is a density (or atom arrangement) that may be obtained from a density | ||
| Line 12: | Line 12: | ||
that in the basic structure the modulation is occupational. | that in the basic structure the modulation is occupational. | ||
| − | ==See also== | + | == See also == |
[[Displacive modulation]] | [[Displacive modulation]] | ||
| − | [[Image:BO01F05.gif]] | + | [[Image:BO01F05.gif]] |
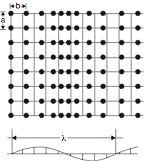
| − | Figure Caption: Model for a displacively modulated crystal structure. The basic structure | + | Figure Caption: Model for a displacively modulated crystal structure. The basic structure is two-dimensional rectangular, with lattice constants ''a'' and ''b'', the modulation wave vector is in the ''b''-direction, the wavelength of the periodic modulation is λ such that λ/''b'' is an irrational number.]] |
| − | is two-dimensional rectangular, with lattice constants ''a'' and ''b'', the modulation | + | |
| − | wave vector is in the ''b''-direction, the wavelength of the periodic modulation | + | [[Category:Fundamental crystallography]] |
| − | is λ such that λ/''b'' is an irrational number. | ||
Revision as of 17:05, 6 February 2012
Structure cristalline modulée (Fr.), Struttura cristallina modulata (It), 変調構造 (Ja)
Definition
A modulated crystal structure is a density (or atom arrangement) that may be obtained from a density (or atom arrangement) with space-group symmetry by a finite density change (or finite displacement of each atom, respectively) that is (quasi)periodic. A function or a displacement field is periodic if it is invariant under a lattice of translations. Then its Fourier transform consists of δ-peaks on a reciprocal lattice that spans the space and is nowhere dense. A quasiperiodic function has a Fourier transform consisting of δ-peaks on a vector module of finite rank. This means that the peaks may be indexed with integers using a finite number of basis vectors. If the modulation consists of deviations from the basic structure in the positions, the modulation is displacive (displacive modulation, see Figure.). When the probability distribution deviates from that in the basic structure the modulation is occupational.
See also
Figure Caption: Model for a displacively modulated crystal structure. The basic structure is two-dimensional rectangular, with lattice constants a and b, the modulation wave vector is in the b-direction, the wavelength of the periodic modulation is λ such that λ/b is an irrational number.]]