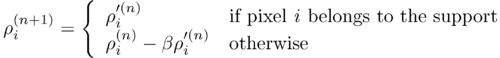Difference between revisions of "Hybrid input-output algorithm"
From Online Dictionary of Crystallography
| Line 5: | Line 5: | ||
Be <math>\rho^{(n)}</math> a trial scattering density in <math>n^{th}</math> iteration cycle. Be <math>\rho'^{(n)}</math> a density obtained from <math>\rho^{(n)}</math> by Fourier-transforming <math>\rho^{(n)}</math>, replacing all Fourier amplitudes by the experimentally observed amplitudes, and applying inverse Fourier transform. Then the density <math>\rho^{(n+1)}</math> is defined pixel-wise by the following scheme: | Be <math>\rho^{(n)}</math> a trial scattering density in <math>n^{th}</math> iteration cycle. Be <math>\rho'^{(n)}</math> a density obtained from <math>\rho^{(n)}</math> by Fourier-transforming <math>\rho^{(n)}</math>, replacing all Fourier amplitudes by the experimentally observed amplitudes, and applying inverse Fourier transform. Then the density <math>\rho^{(n+1)}</math> is defined pixel-wise by the following scheme: | ||
| − | [[Image:CF_4.png|500px|center]] | + | <br>[[Image:CF_4.png|500px|center]]<br> |
In crystallography, the support is usually not known <math>\textit{a~priori}</math>, and a dynamical support must be used, <math>\textit{i.e.}</math> the support is newly defined in each iteration cycle based on predefined criterion. | In crystallography, the support is usually not known <math>\textit{a~priori}</math>, and a dynamical support must be used, <math>\textit{i.e.}</math> the support is newly defined in each iteration cycle based on predefined criterion. | ||
Revision as of 14:16, 27 August 2013
Definition
An algorithm proposed by R. Fienup in 1982. The original application of the algorithm was the phase retrieval of diffraction patterns of non-periodic objects. However, the algorithm or its components have been used several times also in crystallography.
Be [math]\rho^{(n)}[/math] a trial scattering density in [math]n^{th}[/math] iteration cycle. Be [math]\rho'^{(n)}[/math] a density obtained from [math]\rho^{(n)}[/math] by Fourier-transforming [math]\rho^{(n)}[/math], replacing all Fourier amplitudes by the experimentally observed amplitudes, and applying inverse Fourier transform. Then the density [math]\rho^{(n+1)}[/math] is defined pixel-wise by the following scheme:
In crystallography, the support is usually not known [math]\textit{a~priori}[/math], and a dynamical support must be used, [math]\textit{i.e.}[/math] the support is newly defined in each iteration cycle based on predefined criterion.