Difference between revisions of "Modulated crystal structure"
From Online Dictionary of Crystallography
m (removed double point, link decoration, italics, internal links added) |
BrianMcMahon (talk | contribs) m (Style edits to align with printed edition) |
||
| Line 1: | Line 1: | ||
| − | <Font color="blue">Structure cristalline modulée</font> (Fr. | + | <Font color="blue">Structure cristalline modulée</font> (''Fr''). <Font color="black">Struttura cristallina modulata </Font>(''It''). <Font color="purple"> 変調構造 </Font>(''Ja''). |
== Definition == | == Definition == | ||
| Line 9: | Line 9: | ||
δ-peaks on a reciprocal lattice that spans the space and is nowhere dense. A quasiperiodic | δ-peaks on a reciprocal lattice that spans the space and is nowhere dense. A quasiperiodic | ||
function has a Fourier transform consisting of δ-peaks on a vector module of finite rank. This means that the peaks may be indexed with integers using a finite number of basis vectors. If the modulation consists of deviations from the basic structure in the positions, | function has a Fourier transform consisting of δ-peaks on a vector module of finite rank. This means that the peaks may be indexed with integers using a finite number of basis vectors. If the modulation consists of deviations from the basic structure in the positions, | ||
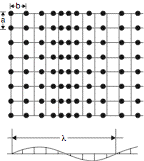
| − | the modulation is [[displacive modulation|''displacive'']] (see | + | the modulation is [[displacive modulation|''displacive'']] (see figure). When the probability distribution deviates from |
that in the basic structure the modulation is ''occupational''. | that in the basic structure the modulation is ''occupational''. | ||
[[Image:BO01F05.gif]] | [[Image:BO01F05.gif]] | ||
| − | + | Model for a displacively modulated crystal structure. The basic structure is two-dimensional rectangular, with lattice constants ''a'' and ''b'', the modulation wave vector is in the ''b''-direction, the wavelength of the periodic modulation is λ such that λ/''b'' is an irrational number. | |
== See also == | == See also == | ||
| − | [[Displacive modulation]] | + | *[[Displacive modulation]] |
| − | [[Modular crystal structure]] | + | *[[Modular crystal structure]] |
[[Category:Fundamental crystallography]] | [[Category:Fundamental crystallography]] | ||
Revision as of 17:01, 15 May 2017
Structure cristalline modulée (Fr). Struttura cristallina modulata (It). 変調構造 (Ja).
Definition
A modulated crystal structure is a density (or atom arrangement) that may be obtained from a density (or atom arrangement) with space-group symmetry by a finite density change (or finite displacement of each atom, respectively) that is (quasi)periodic. A function or a displacement field is periodic if it is invariant under a lattice of translations. Then its Fourier transform consists of δ-peaks on a reciprocal lattice that spans the space and is nowhere dense. A quasiperiodic function has a Fourier transform consisting of δ-peaks on a vector module of finite rank. This means that the peaks may be indexed with integers using a finite number of basis vectors. If the modulation consists of deviations from the basic structure in the positions, the modulation is displacive (see figure). When the probability distribution deviates from that in the basic structure the modulation is occupational.
Model for a displacively modulated crystal structure. The basic structure is two-dimensional rectangular, with lattice constants a and b, the modulation wave vector is in the b-direction, the wavelength of the periodic modulation is λ such that λ/b is an irrational number.