Difference between revisions of "Superspace"
From Online Dictionary of Crystallography
(+cat, lang.) |
BrianMcMahon (talk | contribs) (Tidied translations and added German and Spanish (U. Mueller)) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | < | + | <font color="blue">Superespace, hyperespace</font> (''Fr''). <font color="red">Superraum</font> (''Ge''). <font color="black">Superspazio</font> (''It''). <font color="purple">超空間</font> (''Ja''). <font color="green">Superespacio</font> (''Sp''). |
| + | |||
== Definition == | == Definition == | ||
| Line 8: | Line 9: | ||
== Applications == | == Applications == | ||
| − | Superspace is used to describe quasi-periodic structures ( | + | Superspace is used to describe quasi-periodic structures (see [[aperiodic crystal]]). We denote the dimension of the physical space |
by ''m''. Then a function ρ('''r''') is quasi-periodic if its Fourier transform is given by | by ''m''. Then a function ρ('''r''') is quasi-periodic if its Fourier transform is given by | ||
| Line 15: | Line 16: | ||
where the ''Fourier module'' ''M''<sup>*</sup> is the set of vectors (Z-module) of the form | where the ''Fourier module'' ''M''<sup>*</sup> is the set of vectors (Z-module) of the form | ||
| − | <math> k~=~\sum_{i=1}^n h_i a_i^* | + | <math> k~=~\sum_{i=1}^n h_i a_i^* ~~~(h_i~{\rm integers}),</math> |
for a basis '''a'''<sub>i</sub><sup>*</sup> with the property that <math>\sum_i h_i a_i^*=0</math> implies ''h''<sub>i</sub>=0 (all ''i'') if the indices | for a basis '''a'''<sub>i</sub><sup>*</sup> with the property that <math>\sum_i h_i a_i^*=0</math> implies ''h''<sub>i</sub>=0 (all ''i'') if the indices | ||
| Line 22: | Line 23: | ||
The vectors r<sub>s</sub> have two components: '''r''' and '''r'''<sub>''I''</sub>. The relation is written as | The vectors r<sub>s</sub> have two components: '''r''' and '''r'''<sub>''I''</sub>. The relation is written as | ||
| − | <math>r_s~=~( r,~ r_I)</math> | + | <math>r_s~=~( r,~ r_I).</math> |
In the superspace there is a reciprocal basis '''a'''<sub>si</sub><sup>*</sup> such that '''a'''<sub>i</sub><sup>*</sup> is the projection of '''a'''<sub>si</sub><sup>*</sup> on the subspace ''V''<sub>E</sub>. | In the superspace there is a reciprocal basis '''a'''<sub>si</sub><sup>*</sup> such that '''a'''<sub>i</sub><sup>*</sup> is the projection of '''a'''<sub>si</sub><sup>*</sup> on the subspace ''V''<sub>E</sub>. | ||
| Line 39: | Line 40: | ||
ρ<sub>s</sub>(r<sub>s</sub>) is lattice periodic. Its direct lattice Σ is the dual of Σ<sup>*</sup> and its basis | ρ<sub>s</sub>(r<sub>s</sub>) is lattice periodic. Its direct lattice Σ is the dual of Σ<sup>*</sup> and its basis | ||
vectors are ''a''<sub>is</sub> satisfying ''a''<sub>si</sub>.''a''<sub>sj</sub><sup>*</sup> = δ<sub>ij</sub>. Therefore, the symmetry group | vectors are ''a''<sub>is</sub> satisfying ''a''<sub>si</sub>.''a''<sub>sj</sub><sup>*</sup> = δ<sub>ij</sub>. Therefore, the symmetry group | ||
| − | of ρ<sub>s</sub>(r<sub>s</sub>) is a space | + | of ρ<sub>s</sub>(r<sub>s</sub>) is a space group in the ''n''-dimensional superspace, where the dimension ''n'' is equal to the rank |
of the Fourier module. In the superspace the usual crystallographic notions and techniques may be applied. For point atoms, the function ρ<sub>s</sub>(r<sub>s</sub>) is concentrated on surfaces | of the Fourier module. In the superspace the usual crystallographic notions and techniques may be applied. For point atoms, the function ρ<sub>s</sub>(r<sub>s</sub>) is concentrated on surfaces | ||
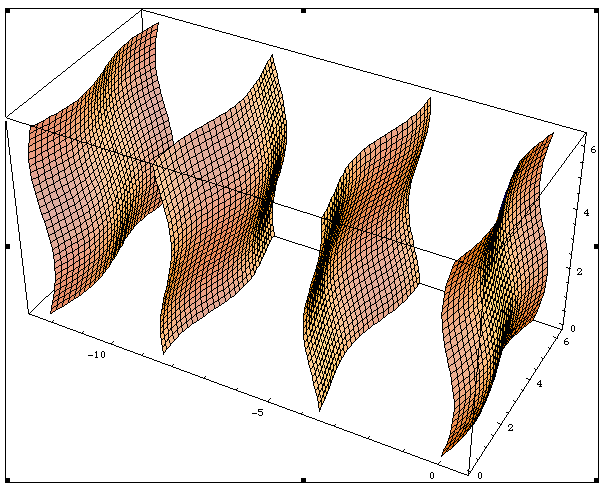
| − | of co-dimension equal to the dimension of the physical space ( | + | of co-dimension equal to the dimension of the physical space (see figure). |
| − | [[Image:IncEmbed.gif | + | [[Image:IncEmbed.gif|frame|An example of the embedding of a one-dimensional modulated chain with two modulation wave vectors. It consists of an array of two-dimensional surfaces, with three-dimensional lattice periodicity. The intersection of the surfaces with the physical space (a line) gives the positions of the modulated structure.|right]] |
| − | |||
| − | |||
| − | wave vectors. It consists of an array of two-dimensional surfaces, with three-dimensional | ||
| − | lattice periodicity. The intersection of the surfaces with the physical space (a line) gives | ||
| − | the positions of the modulated structure. | ||
[[Category: Fundamental crystallography]] | [[Category: Fundamental crystallography]] | ||
Latest revision as of 09:07, 20 November 2017
Superespace, hyperespace (Fr). Superraum (Ge). Superspazio (It). 超空間 (Ja). Superespacio (Sp).
Definition
Superspace is a Euclidean vector space with a preferred (real) subspace VE that has the dimension of the physical space, usually three, but two for surfaces, and one for line structures.
Applications
Superspace is used to describe quasi-periodic structures (see aperiodic crystal). We denote the dimension of the physical space by m. Then a function ρ(r) is quasi-periodic if its Fourier transform is given by
\rho( r)~=~\sum_{ k \in M^*} \hat{\rho}( k \exp (2\pi i k. r ),
where the Fourier module M* is the set of vectors (Z-module) of the form
k~=~\sum_{i=1}^n h_i a_i^* ~~~(h_i~{\rm integers}),
for a basis ai* with the property that \sum_i h_i a_i^*=0 implies hi=0 (all i) if the indices hi are integers. The number n of basis vectors is the rank of the Fourier module.
The vectors rs have two components: r and rI. The relation is written as
r_s~=~( r,~ r_I).
In the superspace there is a reciprocal basis asi* such that ai* is the projection of asi* on the subspace VE. The reciprocal lattice Σ in superspace then is projected on the Fourier module M*. The function ρ(r) then can be embedded as
\rho_s(r_s)~=~\sum_{k_s\in\Sigma^*} \hat{\rho}(\pi k_s= k) \exp (2\pi i k_s.r_s).
The function ρ(r) is the restriction of ρs(rs) to the subspace
\rho( r)~=~\rho_s( r,0).
Because the Fourier components in superspace belong to reciprocal vectors of Σ*, the function
ρs(rs) is lattice periodic. Its direct lattice Σ is the dual of Σ* and its basis
vectors are ais satisfying asi.asj* = δij. Therefore, the symmetry group
of ρs(rs) is a space group in the n-dimensional superspace, where the dimension n is equal to the rank
of the Fourier module. In the superspace the usual crystallographic notions and techniques may be applied. For point atoms, the function ρs(rs) is concentrated on surfaces
of co-dimension equal to the dimension of the physical space (see figure).