Difference between revisions of "Sohncke groups"
From Online Dictionary of Crystallography
BrianMcMahon (talk | contribs) m (Tidied translations.) |
(reformulation) |
||
| Line 3: | Line 3: | ||
[[Image:Sohncke-vs-chiral-scheme.png|500px|Classification scheme of space groups in three-dimensional space in terms of chirality.|right]] | [[Image:Sohncke-vs-chiral-scheme.png|500px|Classification scheme of space groups in three-dimensional space in terms of chirality.|right]] | ||
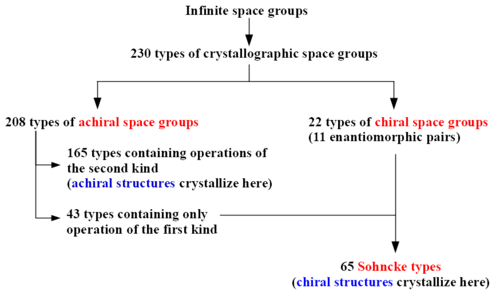
| − | '''Sohncke groups''' are the | + | '''Sohncke groups''' are the three-dimensional [[space group]]s containing only operations of the first kind (rotations, rototranslations, translations). Among the 230 types of space groups, 65 are Sohncke types. [[Chirality|Chiral]] [[crystal structure]]s, including proteins, occur in these groups, not only in the [[chiral space group]]s. |
The term comes from Leonhard Sohncke (Halle, 22 February 1842 – München, 1 November 1897), German mathematician, whose derivation was based on the results previously published by Marie Ennemond Camille Jordan (Lyon, 5 January 1838 – Paris, 22 January 1922), French mathematician. | The term comes from Leonhard Sohncke (Halle, 22 February 1842 – München, 1 November 1897), German mathematician, whose derivation was based on the results previously published by Marie Ennemond Camille Jordan (Lyon, 5 January 1838 – Paris, 22 January 1922), French mathematician. | ||
Revision as of 03:12, 28 November 2018
Groupes de Sohncke (Fr). Sohncke-Raumgruppe (Ge). Gruppi di Sohncke (It). ソンケ群 (Ja). Grupos de Sohncke (Sp).
Sohncke groups are the three-dimensional space groups containing only operations of the first kind (rotations, rototranslations, translations). Among the 230 types of space groups, 65 are Sohncke types. Chiral crystal structures, including proteins, occur in these groups, not only in the chiral space groups.
The term comes from Leonhard Sohncke (Halle, 22 February 1842 – München, 1 November 1897), German mathematician, whose derivation was based on the results previously published by Marie Ennemond Camille Jordan (Lyon, 5 January 1838 – Paris, 22 January 1922), French mathematician.
References
- Jordan, C. (1869). Annali di Matematica Pura ed Applicata (1867-1897), 2, 167-215. Mémoire sur les groupes de mouvements.
- Sohncke, L. (1879). Entwickelung einer Theorie der Krystallstruktur. B. G. Teubner, Leipzig