Difference between revisions of "Bravais-Miller indices"
From Online Dictionary of Crystallography
AndreAuthier (talk | contribs) |
BrianMcMahon (talk | contribs) m (Tidied translations.) |
||
| (10 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | ( | + | <font color="blue">Indices de Bravais-Miller</font> (''Fr''). <font color="black">Indici di Bravais-Miller</font> (''It''). <font color="purple">ブラベー・ミラー指数</font> (''Ja''). <font color="green">Indices de Bravais-Miller</font> (''Sp''). |
| + | <Font color="black"> | ||
== Definition == | == Definition == | ||
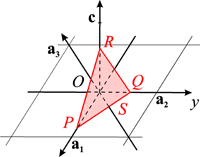
| − | + | For trigonal and hexagonal crystals, it is useful to use a reference built on four axes, three in the plane normal to the unique axis ('''a<sub>1</sub>''', '''a<sub>2</sub>''', '''a<sub>3</sub>''') and one ( '''c''') for the unique axis. Consequently, four indices of lattice planes (''hkil'') are used, called the '''Bravais-Miller indices'''. Here ''h'', ''k'', ''i'', ''l'' are integers inversely proportional to the intercepts of a plane of the family with the four axes. | |
| + | Only two of the three axes in a plane are linearly independent: '''a<sub>3</sub>''' is expressed as '''a<sub>3</sub>''' = -'''a<sub>1</sub>'''-'''a<sub>2</sub>'''. Analogously, the indices ''h'', ''k'', ''i'' are cyclically permutable and related by | ||
<center> | <center> | ||
| − | ''h'' + ''k'' + ''i'' = 0 | + | ''h'' + ''k'' + ''i'' = 0. |
</center> | </center> | ||
| Line 13: | Line 15: | ||
== see also == | == see also == | ||
| − | [[Miller indices]] | + | *[[Miller indices]] |
| − | + | *[[Weber indices]] | |
| − | |||
[[Category:Fundamental crystallography]]<br> | [[Category:Fundamental crystallography]]<br> | ||
| + | [[Category:Morphological crystallography]] | ||
Latest revision as of 16:46, 9 November 2017
Indices de Bravais-Miller (Fr). Indici di Bravais-Miller (It). ブラベー・ミラー指数 (Ja). Indices de Bravais-Miller (Sp).
Definition
For trigonal and hexagonal crystals, it is useful to use a reference built on four axes, three in the plane normal to the unique axis (a1, a2, a3) and one ( c) for the unique axis. Consequently, four indices of lattice planes (hkil) are used, called the Bravais-Miller indices. Here h, k, i, l are integers inversely proportional to the intercepts of a plane of the family with the four axes. Only two of the three axes in a plane are linearly independent: a3 is expressed as a3 = -a1-a2. Analogously, the indices h, k, i are cyclically permutable and related by
h + k + i = 0.