Difference between revisions of "Mapping"
From Online Dictionary of Crystallography
BrianMcMahon (talk | contribs) m (Tidied translations.) |
|||
| (5 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| + | <font color="blue">Transformation</font> (''Fr''). <font color="red">Abbildung</font> (''Ge''). <font color="black">Trasformazione</font> (''It''). <font color="purple">写像</font> (''Ja''). <font color="green">Transformación geométrica</font> (''Sp''). | ||
| + | |||
| + | |||
The term '''mapping''' is often used in mathematics as a synonym of ''function''. In crystallography it is particularly used to indicate a ''transformation''. | The term '''mapping''' is often used in mathematics as a synonym of ''function''. In crystallography it is particularly used to indicate a ''transformation''. | ||
==Domain, image and codomain== | ==Domain, image and codomain== | ||
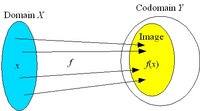
| − | [[Image:Domain.jpg|thumb|200px|Definition of domain, image and codomain]] A mapping ''f'' of ''X'' to ''Y'' (''f'' : ''X'' | + | [[Image:Domain.jpg|thumb|200px|Definition of domain, image and codomain.]] A '''mapping''' ''f'' of ''X'' to ''Y'' (''f'' : ''X'' → ''Y'') assigns to each element ''x'' in the '''domain''' ''X'' a value ''y'' in the '''codomain''' ''Y''. |
| − | The set of values ''f''(''X'') is the '''image''' of the | + | The set of values ''f''(''X'') = { ''f''(''x'') : ''x'' in ''X'' } is the '''image''' of the mapping. The image may be the whole codomain or a proper subset of it. |
| + | |||
| + | For an element ''y'' in the image of ''f'', the set { ''x'' in ''X'' : ''f''(''x'') = ''y'' } of elements mapped to ''y'' is called the '''preimage''' of ''y'', denoted by ''f''<sup>−1</sup>{''y''}. Also, the single elements in ''f''<sup>−1</sup>{''y''} are | ||
| + | called '''preimages''' of ''x''. | ||
==Surjective, injective and bijective mappings== | ==Surjective, injective and bijective mappings== | ||
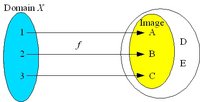
| − | [[Image:Surjection.jpg|thumb|200px|In a surjective mapping the image | + | [[Image:Surjection.jpg|thumb|200px|In a surjective mapping the image is the whole codomain.]] The mapping ''f'' is '''surjective''' ('''onto''') if the image coincides with the codomain. The mapping may be '''many-to-one''' because more than one element of the domain ''X'' can be mapped to the same element of the codomain ''Y'', but every element of ''Y'' has a preimage in ''X''. A surjective mapping is a '''surjection'''. |
| − | |||
| − | |||
| − | |||
| + | [[Image:Injection.jpg|thumb|200px|An injective mapping is a one-to-one mapping.]] The mapping ''f'' is '''injective''' ('''one-to-one mapping''') if different elements of the domain ''X'' are mapped to different elements in the codomain ''Y''. The image does not have to coincide with the codomain and therefore there may be elements of ''Y'' that are not mapped to some elements of ''X''. An injective mapping is an '''injection'''. | ||
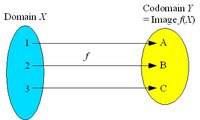
| − | [[Image:Bijection.jpg|thumb|200px|A bijective mapping is a one-to-one correspondence]] The mapping ''f'' is '''bijective''' ('''one-to-one correspondence''') if and only if it is both injective and surjective. Every element of the codomain ''Y'' | + | [[Image:Bijection.jpg|thumb|200px|A bijective mapping is a one-to-one correspondence.]] The mapping ''f'' is '''bijective''' ('''one-to-one correspondence''') if and only if it is both injective and surjective. Every element of the codomain ''Y'' has exactly one preimage in the domain ''X''. The image coincides with the codomain. A bijective mapping is a '''bijection'''. |
| + | <br> | ||
| + | If the codomain of an injective mapping ''f'' is restricted to the image ''f''(''X''), the resulting mapping is a bijection from ''X'' to ''f''(''X''). | ||
[[Category:Fundamental crystallography]] | [[Category:Fundamental crystallography]] | ||
Latest revision as of 09:08, 11 December 2017
Transformation (Fr). Abbildung (Ge). Trasformazione (It). 写像 (Ja). Transformación geométrica (Sp).
The term mapping is often used in mathematics as a synonym of function. In crystallography it is particularly used to indicate a transformation.
Domain, image and codomain
A mapping f of X to Y (f : X → Y) assigns to each element x in the domain X a value y in the codomain Y.The set of values f(X) = { f(x) : x in X } is the image of the mapping. The image may be the whole codomain or a proper subset of it.
For an element y in the image of f, the set { x in X : f(x) = y } of elements mapped to y is called the preimage of y, denoted by f−1{y}. Also, the single elements in f−1{y} are called preimages of x.
Surjective, injective and bijective mappings
The mapping f is surjective (onto) if the image coincides with the codomain. The mapping may be many-to-one because more than one element of the domain X can be mapped to the same element of the codomain Y, but every element of Y has a preimage in X. A surjective mapping is a surjection.
If the codomain of an injective mapping f is restricted to the image f(X), the resulting mapping is a bijection from X to f(X).