Difference between revisions of "Mapping"
From Online Dictionary of Crystallography
BrianMcMahon (talk | contribs) (Tidied translations and added German and Spanish (U. Mueller)) |
BrianMcMahon (talk | contribs) m (Tidied translations.) |
||
| Line 1: | Line 1: | ||
| − | <font color="blue">Transformation </font>(''Fr''). <font color="red">Abbildung</font> (''Ge''). <font color="black">Trasformazione </font>(''It''). <font color="purple">写像</font>(''Ja''). <font color="green">Transformación geométrica</font> (''Sp''). | + | <font color="blue">Transformation</font> (''Fr''). <font color="red">Abbildung</font> (''Ge''). <font color="black">Trasformazione</font> (''It''). <font color="purple">写像</font> (''Ja''). <font color="green">Transformación geométrica</font> (''Sp''). |
Latest revision as of 09:08, 11 December 2017
Transformation (Fr). Abbildung (Ge). Trasformazione (It). 写像 (Ja). Transformación geométrica (Sp).
The term mapping is often used in mathematics as a synonym of function. In crystallography it is particularly used to indicate a transformation.
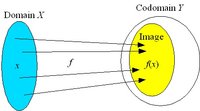
Domain, image and codomain
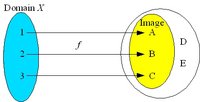
A mapping f of X to Y (f : X → Y) assigns to each element x in the domain X a value y in the codomain Y.The set of values f(X) = { f(x) : x in X } is the image of the mapping. The image may be the whole codomain or a proper subset of it.
For an element y in the image of f, the set { x in X : f(x) = y } of elements mapped to y is called the preimage of y, denoted by f−1{y}. Also, the single elements in f−1{y} are called preimages of x.
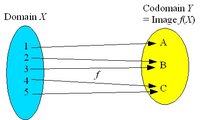
Surjective, injective and bijective mappings
The mapping f is surjective (onto) if the image coincides with the codomain. The mapping may be many-to-one because more than one element of the domain X can be mapped to the same element of the codomain Y, but every element of Y has a preimage in X. A surjective mapping is a surjection.
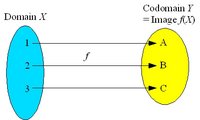
If the codomain of an injective mapping f is restricted to the image f(X), the resulting mapping is a bijection from X to f(X).