Difference between revisions of "Sohncke groups"
From Online Dictionary of Crystallography
(reformulation) |
(Link to external resources) |
||
| Line 8: | Line 8: | ||
== References == | == References == | ||
| − | * Jordan, C. (1869). ''Annali di Matematica Pura ed Applicata (1867-1897)'', '''2''', 167-215. ''Mémoire sur les groupes de mouvements''. | + | * Jordan, C. (1869). ''Annali di Matematica Pura ed Applicata (1867-1897)'', '''2''' (2), 167-215. ''Mémoire sur les groupes de mouvements'' ([http://iris.univ-lille1.fr/handle/1908/1921 link to the issue of the journal containing the paper by Jordan]). |
* Sohncke, L. (1879). ''Entwickelung einer Theorie der Krystallstruktur''. B. G. Teubner, Leipzig | * Sohncke, L. (1879). ''Entwickelung einer Theorie der Krystallstruktur''. B. G. Teubner, Leipzig | ||
Revision as of 20:25, 28 November 2018
Groupes de Sohncke (Fr). Sohncke-Raumgruppe (Ge). Gruppi di Sohncke (It). ソンケ群 (Ja). Grupos de Sohncke (Sp).
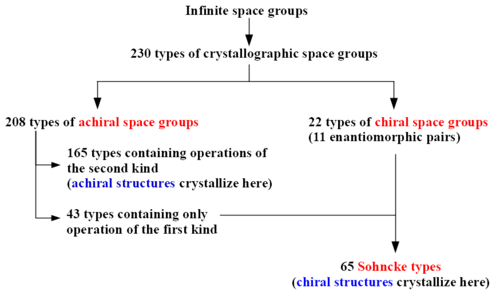
Sohncke groups are the three-dimensional space groups containing only operations of the first kind (rotations, rototranslations, translations). Among the 230 types of space groups, 65 are Sohncke types. Chiral crystal structures, including proteins, occur in these groups, not only in the chiral space groups.
The term comes from Leonhard Sohncke (Halle, 22 February 1842 – München, 1 November 1897), German mathematician, whose derivation was based on the results previously published by Marie Ennemond Camille Jordan (Lyon, 5 January 1838 – Paris, 22 January 1922), French mathematician.
References
- Jordan, C. (1869). Annali di Matematica Pura ed Applicata (1867-1897), 2 (2), 167-215. Mémoire sur les groupes de mouvements (link to the issue of the journal containing the paper by Jordan).
- Sohncke, L. (1879). Entwickelung einer Theorie der Krystallstruktur. B. G. Teubner, Leipzig