Mapping

The term mapping is often used in mathematics as a synonym of function. In crystallography it is particularly used to indicate a transformation.

Domain, image and codomain

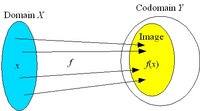
Definition of domain, image and codomain

A mapping f of X to Y (f : X → Y) acts on a domain X and the result is defined in the codomain Y of the function.

The set of values f(X) is the image of the function. The image may span the whole codomain or be a subset of it.

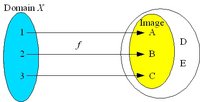
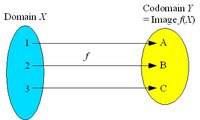
Surjective, injective and bijective mappings

In a surjective mapping the image spans the whole codomain

The mapping f is surjective (onto) if the image coincides with the codomain. The mapping is many-to-one because more than one element of the domain X can be mapped to the same element of the codomain Y, but all elements of Y are mapped to some elements of X. A surjective mapping is a surjection.

An injective mapping is a one-to-one mapping

The mapping f is injective (one-to-one mapping) if different elements of the domain X are mapped to different elements in the codomain Y. The image does not have to coincide with the codomain and therefore there may be elements of Y that are not mapped to some elements of X. An injective mapping is an injection.

A bijective mapping is a one-to-one correspondence

The mapping f is bijective (one-to-one correspondence) if and only if it is both injective and surjective. Every element of the codomain Y is mapped to exactly one element of the domain X. The image coincides with the codomain. A bijective function is a bijection.