Difference between revisions of "Atomic surface"
From Online Dictionary of Crystallography
TedJanssen (talk | contribs) |
BrianMcMahon (talk | contribs) m |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
<Font color="blue">Surface atomique, fenêtre, domaine d'acceptation </font>(Fr.) | <Font color="blue">Surface atomique, fenêtre, domaine d'acceptation </font>(Fr.) | ||
| − | + | == Definition == | |
Quasiperiodic structures may be considered as the intersection of a higher-dimensional | Quasiperiodic structures may be considered as the intersection of a higher-dimensional | ||
| Line 22: | Line 18: | ||
windows, atomic surfaces, or acceptance domains). | windows, atomic surfaces, or acceptance domains). | ||
| − | + | == See also == | |
| + | [[Superspace]], [[acceptance domain]] | ||
[[Image:IncEmbed.gif]] | [[Image:IncEmbed.gif]] | ||
Revision as of 15:25, 30 June 2010
Surface atomique, fenêtre, domaine d'acceptation (Fr.)
Definition
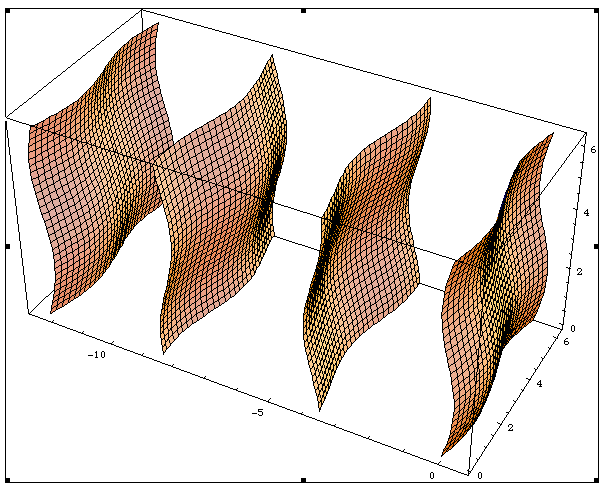
Quasiperiodic structures may be considered as the intersection of a higher-dimensional lattice periodic structure and the physical space. For point atoms or the vertices of a tiling, the higher-dimensional structure consists of a periodic array of objects with a dimension equal to n-m, the difference between the rank of the Fourier module and the dimension of the physical space (usually three), and transverse ( i.e. not tangential) to the physical space. The atomic surface is the (n-m)-dimensional object in superspace (see there) corresponding to a point atom in physical space.
For incommensurately modulated crystals with a smooth modulation function, these atomic surfaces are unbounded (cf. Fig. \ref{embed}). They have the same dimension as the internal space and they have lattice periodicity. For other aperiodic crystals, the atomic surfaces consists of disjoint components, the atomic domains (also called windows, atomic surfaces, or acceptance domains).
See also
Figure Caption. A one-dimensional incommensurate phase with a two-dimensional modulation is the intersection of the one-dimensional physical space with an periodic array of two-dimensional surfaces, with three-dimenisonal lattice periodicity.