Difference between revisions of "Atomic surface"
From Online Dictionary of Crystallography
BrianMcMahon (talk | contribs) m |
m |
||
| Line 10: | Line 10: | ||
Figure Caption. | Figure Caption. | ||
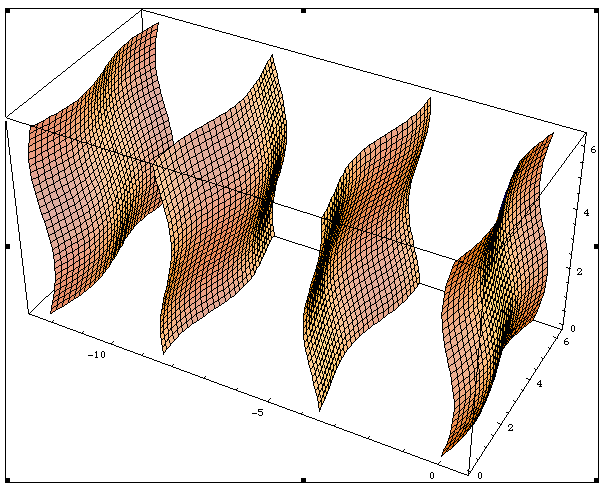
| − | A one-dimensional incommensurate phase with a two-dimensional modulation is the intersection of the one-dimensional physical space with | + | A one-dimensional incommensurate phase with a two-dimensional modulation is the intersection of the one-dimensional physical space with a periodic array of two-dimensional surfaces, with three-dimensional lattice periodicity. |
== See also == | == See also == | ||
[[Superspace]], [[acceptance domain]] | [[Superspace]], [[acceptance domain]] | ||
Revision as of 15:35, 7 July 2014
Surface atomique, fenêtre, domaine d'acceptation (Fr.)
Definition
Quasiperiodic structures may be considered as the intersection of a higher-dimensional lattice periodic structure and the physical space. For point atoms or the vertices of a tiling, the higher-dimensional structure consists of a periodic array of objects with a dimension equal to n-m, the difference between the rank of the Fourier module and the dimension of the physical space (usually three), and transverse ( i.e. not tangential) to the physical space. The atomic surface is the (n-m)-dimensional object in superspace (see there) corresponding to a point atom in physical space.
For incommensurately modulated crystals with a smooth modulation function, these atomic surfaces are unbounded (cf. Figure). They have the same dimension as the internal space and they have lattice periodicity. For other aperiodic crystals, the atomic surfaces consists of disjoint components, the atomic domains (also called windows, atomic surfaces, or acceptance domains).
Figure Caption. A one-dimensional incommensurate phase with a two-dimensional modulation is the intersection of the one-dimensional physical space with a periodic array of two-dimensional surfaces, with three-dimensional lattice periodicity.