Difference between revisions of "Bragg's law"
From Online Dictionary of Crystallography
m (Lang (Ar)) |
(correction (there is an internal link about that!). Also, added Ru) |
||
| Line 1: | Line 1: | ||
| − | <Font color="blue">Loi de Bragg</Font> (''Fr'') | + | <font color="orange">قانون برافي</font> (''Ar''); <Font color="blue">Loi de Bragg</Font> (''Fr''); <Font color="red">Bragg Gesetz</Font> (''Ge''); <Font color="black"> Legge di Bragg</Font> (''It''); <Font color="purple">ブラッグの法則 </Font>(''Ja''); <Font color="brown">Условие Вульфа — Брэгга</Font> (''Ru''); <Font color="green">Ley de Bragg</Font> (''Sp''). |
== Definition == | == Definition == | ||
| Line 10: | Line 10: | ||
</center> | </center> | ||
| − | where ''d'' is the | + | where ''d'' is the [[interplanar spacing]], θ the angle between the wave vector of the incident plane wave, '''k<sub>o</sub>''', and the lattice planes, λ its wavelength and ''n'' is an integer, the order of the reflection. It is equivalent to the [[Reciprocal lattice#Diffraction condition in reciprocal space|diffraction condition in reciprocal space]] and to the [[Laue equations]]. |
== Direct derivation of Bragg's law == | == Direct derivation of Bragg's law == | ||
Revision as of 14:31, 12 October 2017
قانون برافي (Ar); Loi de Bragg (Fr); Bragg Gesetz (Ge); Legge di Bragg (It); ブラッグの法則 (Ja); Условие Вульфа — Брэгга (Ru); Ley de Bragg (Sp).
Contents
Definition
Bragg's law provides the condition for a plane wave to be diffracted by a family of lattice planes:
2 d sin θ = n λ
where d is the interplanar spacing, θ the angle between the wave vector of the incident plane wave, ko, and the lattice planes, λ its wavelength and n is an integer, the order of the reflection. It is equivalent to the diffraction condition in reciprocal space and to the Laue equations.
Direct derivation of Bragg's law
- Reflection from the first plane
The scattered waves will be in phase whatever the distribution of the point scatterers in the first plane if the angle of the reflected wave vector, kh, is also equal to θ. This is Snell-Descartes' law of reflection.
- Reflection from the second plane
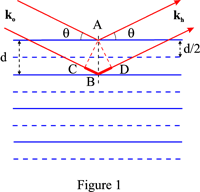
Since the phase of the reflected waves is independent of the position of the point scatterer in the plane, the phase difference between the waves reflected by two successive lattice planes is obtained by choosing arbitrarily a scattering point, A, on the first plane and a scattering point, B, on the second plane such that AB is normal to the planes. If C and D are the projections of A on the incident and reflected wave vectors passing through B, it is clear from Figure 1 that the path difference between the waves reflected at A and B, respectively, is:
CB + BD = 2d sin θ
and that the two waves will be in phase if this path difference is equal to nλ where n is an integer.
- Reflection from the third, etc. planes
If Bragg's relation is satisfied for the first two planes, the waves reflected with wave vector kh will be in phase for all the planes of the family.
Order of the reflection
Bragg's law may also be written:
2 (d/n) sin θ = λ.
One may then say that a Bragg reflection of order n on a family of lattice planes of order n is equivalent to reflection of order 1 on a family of fictitious, or imaginary, planes of lattice spacing
[math]d_{hkl}[/math] = d/n.
This fictitious family is associated with the reciprocal lattice vector OH where OH = n/d = 1/[math]d_{hkl}[/math]. The indices of the reflection are hkl. For instance, the dashed horizontal lines in Figure 1 correspond to the fictitious planes associated with the second order, n = 2.
Reflection conditions
If there is a glide plane or a screw axis normal to the lattice planes, the spacing of the actual reflecting planes is d/2 for a glide plane and (d p/q) for a qp screw axis. Bragg's law should then be written:
2 (d/2) sin θ = n λ ⇒ 2 d sin θ = 2n λ
for a glide plane and
2 (d p/q) sin θ = n λ ⇒ 2 d sin θ = (q/p)n λ
for a screw axis qp.
The reflections of odd order for a glide plane and of order different from (q/p)n for a screw axis are then absent. One speaks of systematic absences related to the presence of glide or screw components.
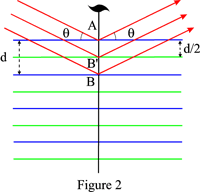
As an example, Figure 2 shows the case of a 21 screw axis: the reflecting planes are the blue planes and the green planes deduced from the latter by the action of the screw axis. Reflections of odd order will be systematically absent.
Influence of deformation
A deformation that leaves a family of lattice planes (hkl) undistorted and its lattice spacing d unchanged will not affect the Bragg angle of kkl reflections, e.g. lattice planes parallel to a screw dislocations.
History
Bragg (1890-1971) presented his derivation of the reflection condition at a meeting of the Cambridge Philosophical Society on 11 November 1912. His paper was published in 1913 [Bragg, W. L. (1913), Proc. Cambridge Phil. Soc. 17, 43-57. The Diffraction of Short Electromagnetic Waves by a Crystal]. For details, see P. P. Ewald (1962), 50 Years of X-ray Diffraction, Utrecht: IUCr/Oosthoek, Section 5, p. 64 and A. Authier (2013), The Early Days of X-ray Diffraction, Oxford: IUCr/Oxford University Press, Section 6.11, p. 120.