Difference between revisions of "Ewald sphere"
From Online Dictionary of Crystallography
BrianMcMahon (talk | contribs) m (Tidied translations.) |
BrianMcMahon (talk | contribs) m (Tidied translations.) |
||
| Line 1: | Line 1: | ||
| − | <font color="blue">Sphère d'Ewald</font> (''Fr''). <font color="red">Ewaldkugel, Ausbreitungskugel</font> (''Ge''). <font color="black">Sfera di Ewald </font>(''It''). <font color="green">Esfera de Ewald</font> (''Sp''). | + | <font color="blue">Sphère d'Ewald</font> (''Fr''). <font color="red">Ewaldkugel, Ausbreitungskugel</font> (''Ge''). <font color="black">Sfera di Ewald</font> (''It''). <font color="green">Esfera de Ewald</font> (''Sp''). |
== Definition == | == Definition == | ||
Revision as of 16:22, 29 November 2017
Sphère d'Ewald (Fr). Ewaldkugel, Ausbreitungskugel (Ge). Sfera di Ewald (It). Esfera de Ewald (Sp).
Contents
Definition
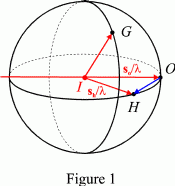
The Ewald sphere, or sphere of reflection, is a sphere of radius 1/λ passing through the origin O of the reciprocal lattice. The incident direction is along a radius of the sphere, IO (Fig. 1). A reflected direction, of unit vector sh, will satisfy the diffraction condition if the diffraction vector OH = IH – IO = sh/λ – so/λ (so unit vector in the direction IO) is a reciprocal lattice vector, namely if H is a node of the reciprocal lattice (see Diffraction condition in reciprocal space). If other reciprocal lattice nodes, such as G, lie also on the sphere, there will be reflected beams along IG, etc. This construction is known as the Ewald construction. When the wavelength is large, there are seldom more than two nodes, O and H, of the reciprocal lattice simultaneously on the Ewald sphere. When there are three or more, one speaks of multiple diffraction, multiple scattering or n-beam diffraction. This situation becomes increasingly frequent as the wavelength decreases and is practically routine for very short wavelengths such as those of γ-rays and electrons. The curvature of the Ewald sphere then becomes negligible and it can often be approximated by a plane. Many reflections must then be taken into account at the same time.
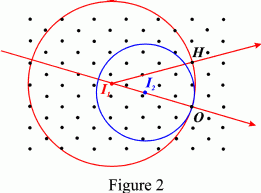
When the wavelength changes, the radius of the Ewald sphere changes. Fig. 2 illustrates the case of the reciprocal (110) lattice plane of a silicon crystal and two Ewald spheres corresponding to Ag Kα (λ1 = 0.709 Å) and Cu Kα (λ2 = 1.54 Å) radiation, respectively. If the incident beam is a white beam, with a wavelength range λmin ≤ λ ≤ λmax, there will be a nest of Ewald spheres of radii 1/λmax ≤ 1/λ ≤ 1/λmin.
Limiting sphere
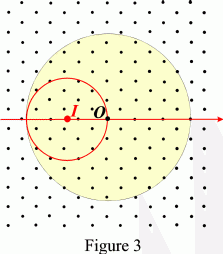
In order to explore the reciprocal space, one rotates the Ewald sphere around the origin, O (in practice one rotates the crystal); as the reciprocal lattice nodes pass through the Ewald sphere, the corresponding reflections are successively excited. It is clear then that the only reflections that can be observed are those for which OH ≤ 2/λ (diameter of the Ewald sphere) and for which the reciprocal nodes lie within a sphere of centre O and radius 2/λ. This sphere is called the limiting sphere (in yellow in Fig. 3). Conversely, if the wavelength of the incident radiation is larger than the largest interplanar spacing dmax of the crystal, there is no reciprocal lattice node within the limiting sphere: no Bragg reflection can take place for λ > dmax.
History
The Ewald sphere was introduced by Ewald in 1913 under the name Ausbreitungskugel or sphere of reflection. [Ewald, P.P. (1913). Physik. Z. 14, 465-472. Zur Theorie der Interferenzen der Röntgentstrahlen in Kristallen. An English translation is given in D. W. J. Cruickshank, H. J. Juretschke and N. Kato, 1992, P. P. Ewald and his dynamical theory of X-ray diffraction. Oxford University Press, IUCr/OUP Book series, Oxford, 114-123). See also P. P. Ewald (1962). IUCr, 50 Years of X-ray Diffraction, Utrecht:IUCr/Oosthoek, Section 15.3, page 250.]
See also
- Chapter 2.2 of International Tables for Crystallography, Volume C