Difference between revisions of "Heavy-atom method"
From Online Dictionary of Crystallography
BrianMcMahon (talk | contribs) |
AndreAuthier (talk | contribs) |
||
| Line 1: | Line 1: | ||
| + | <Font color="blue"> Méthode de l'atome lourd </Font> (''Fr''). | ||
| + | |||
An application of [[Patterson methods]] in crystal [[structure determination]]. For a compound containing a heavy atom (''i.e.'' one with a significantly higher [[atomic scattering factor]] than the others present) the diffraction phases calculated from the position of the heavy atom are used to compute a first approximate [[electron density map]]. Further portions of the structure are recognisable as additional peaks in the map. Successive approximate electron density maps may then be calculated to solve the entire structure. | An application of [[Patterson methods]] in crystal [[structure determination]]. For a compound containing a heavy atom (''i.e.'' one with a significantly higher [[atomic scattering factor]] than the others present) the diffraction phases calculated from the position of the heavy atom are used to compute a first approximate [[electron density map]]. Further portions of the structure are recognisable as additional peaks in the map. Successive approximate electron density maps may then be calculated to solve the entire structure. | ||
Revision as of 05:24, 4 April 2008
Méthode de l'atome lourd (Fr).
An application of Patterson methods in crystal structure determination. For a compound containing a heavy atom (i.e. one with a significantly higher atomic scattering factor than the others present) the diffraction phases calculated from the position of the heavy atom are used to compute a first approximate electron density map. Further portions of the structure are recognisable as additional peaks in the map. Successive approximate electron density maps may then be calculated to solve the entire structure.
Discussion
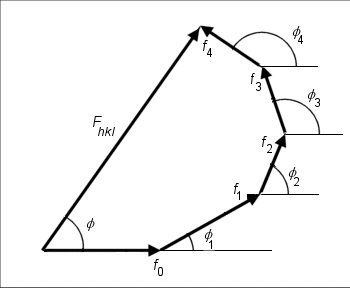
The figure shows how the structure factor is derived by vector addition of the scattered waves from the different contributing atoms in the unit cell. Consider the case of an atom with a very much higher scattering factor than any of the others [math](\,\,f_0 \gt \gt \sum_i f_i \,\,)[/math]; it is clear that the total phase angle [math]\phi[/math] will be small, and that the net phase of the structure factor differs very little from that of the heavy-atom component alone.
If the positions of known heavy atoms can be determined in this way, then the Patterson map, which describes interatomic vectors, allows nearby peaks to be assigned to other atoms in accordance with expected molecular geometry. These are then used in calculating phase angles for the next approximate electron density map.
A practical limitation is that a heavy atom that dominates the vector distribution is also likely to dominate the X-ray scattering as a whole, and overwhelm diffraction peaks from less strongly scattering species.