Law of rational indices
From Online Dictionary of Crystallography
Loi des indices rationnels simples (Fr.). Ley de la racionalidad de los indices (Sp.).
Definition
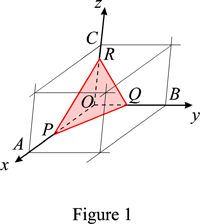
The law of rational indices states that the intercepts, OP, OQ, OR, of the natural faces of a crystal form with the unit-cell axes a, b, c (see Figure 1) are inversely proportional to prime integers, h, k, l. They are called the Miller indices of the face. They are usually small because the corresponding lattice planes are among the densest and have therefore a high interplanar spacing and low indices.
The law of rational indices was deduced by Haüy (1784, 1801) from the observation of the stacking laws required to build up the natural faces of crystals by piling up elementary blocks, for instance cubes to construct the {110} faces of the rhomb-dodecahedron observed in garnets or the ½{210} faces of the pentagon-dodecahedron observed in pyrite, or rhombohedrons to construct the {21.1} (referred to an hegagonal lattice, {[math] 2{\bar 1}0[/math]} referred to a rhombohedral lattice) scalenohedron of calcite.
History
As early as 1773, the Swedish mineralogist T.O. Bergman had observed that the rhombohedron could be deduced by cleavage from the {[math] 2{\bar 1}0[/math]} scalenohedron of calcite, but it is Haüy who showed that the crystal forms could be reconstructed by appropriate stackings of minute cleavage rhomohedrons for calcite and cubes for garnets (Essai d'une théorie sur la structure des cristaux, 1984, Traité de Minéralogie, 1801).