Law of rational indices
From Online Dictionary of Crystallography
Loi des indices rationnels simples (Fr). Gesetz der rationalen Indices (Ge). Legge della razionalità degli indici (It). 有理指数の法則 (Ja). Ley de la racionalidad de los indices (Sp).
Definition
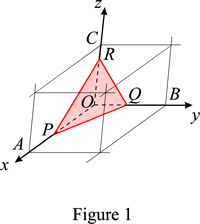
The law of rational indices states that the intercepts, OP, OQ, OR, of the natural faces of a crystal form with the unit-cell axes a, b, c (see Fig. 1) are inversely proportional to prime integers, h, k, l. They are called the Miller indices of the face. They are usually small because the corresponding lattice planes are among the densest and have therefore a high interplanar spacing and low indices.
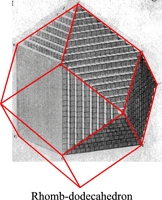
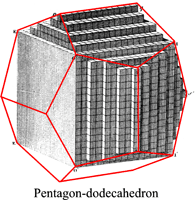
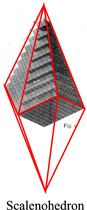
The law of rational indices was deduced by Haüy (1784, 1801) from the observation of the stacking laws required to build the natural faces of crystals by piling up elementary blocks, for instance cubes to construct the {110} faces of the rhomb-dodecahedron observed in garnets or the ½{210} faces of the pentagon-dodecahedron observed in pyrite, or rhombohedrons to construct the {21.1} (referred to an hexagonal lattice, {[math] 2{\bar 1}0[/math]} referred to a rhombohedral lattice) scalenohedron of calcite.
Models from Haüy's Traité de Minéralogie (1801) - the crystal forms have been superimposed in heavy lines.
History
In 1690, C. Huyghens (1629-1695) advanced the hypothesis that the cleavage rhombohedron of calcite was the result of a stacking of flat ellipsoids and used that hypothesis to explain the cleavage properties and the double refraction of calcite. In 1773, the Swedish mineralogist T. O. Bergman (1735-1784) related the cleavage rhombohedron to the {[math] 2{\bar 1}0[/math]} scalenohedron and other forms of calcite, but it is the French mineralogist R.-J. Haüy (1743-1822) who showed that the crystal forms could be reconstructed by appropriate stacking laws of minute cleavage rhombohedra for calcite and cubes for garnets (Essai d'une théorie sur la structure des cristaux, 1784; Traité de Minéralogie, 1801).