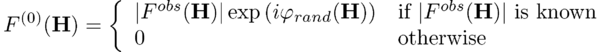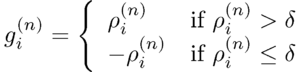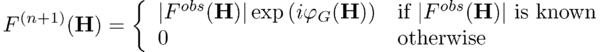Charge flipping
From Online Dictionary of Crystallography
Definition
Charge flipping is a structure solution method from the class of dual-space algorithms. The key component of the charge flipping algorithm is the charge flipping operation. In this operation, all scattering density pixels with density lower than a small positive threshold δ are multiplied by -1 (flipped). In the classical charge flipping algorithm, this direct-space modification is combined with simple resubstitution of structure-factor amplitudes by experimental values, but other modifications and iteration schemes have been proposed and successfully used.
Given a trial scattering density [math]\rho[/math] sampled on a regular grid, and a set of measured structure-factor amplitudes [math]F^{obs}(\mathbf{H})[/math], the basic charge flipping algorithm follows this scheme:
First, the algorithm is initiated in the zeroth cycle by assigning random starting phases [math]\varphi_{rand}(\mathbf{H})[/math] to all experimental amplitudes and making all unobserved amplitudes equal to zero:
The iteration cycle then proceeds as follows:
- The density [math]\rho^{(n)}[/math] is calculated by inverse Fourier transform of [math]F^{(n)}[/math].
- The modified density [math]g^{(n)}[/math] is obtained by flipping the density of all pixels with density values below a certain positive threshold [math]\delta[/math] and keeping the rest of the pixels unchanged:
- Temporary structure factors [math]G^{(n)}(\mathbf{H})=|G^{(n)}(\mathbf{H})|\exp{(i\varphi_{G}(\mathbf{H}))}[/math] are calculated by Fourier transform of [math]g^{(n)}[/math].
- New structure factors [math]F^{(n+1)}[/math] are obtained by combining the experimental amplitudes with the phases [math]\varphi_{G}[/math] and setting all non-measured structure factors to zero:
These modified structure factors then enter the next cycle of iteration.