Group homomorphism
From Online Dictionary of Crystallography
Homomorphisme de groupes (Fr). Gruppenhomomorphismus (Ge). Omomorfismo di gruppi (It). 準同形 (Ja). Homomorfismo de grupos (Sp).
Contents
[hide]Homomorphism between groups
A group homomorphism from a group (G, *) to a group (H, #) is a mapping f : G → H that preserves the composition law, i.e. for all u and v in G one has:
f(u * v) = f(u) # f(v).
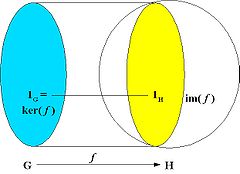
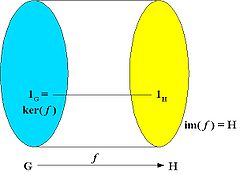
A homomorphism f maps the identity element 1G of G to the identity element 1H of H, and it also maps inverses to inverses: f(u−1) = f(u)−1.
Kernel and image
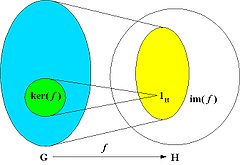
The kernel of the homomorphism f is the set of elements of G that are mapped to the identity of H:
ker(f) = { u in G : f(u) = 1H }.
The image of the homomorphism f is the subset of elements of H to which at least one element of G is mapped by f:
im(f) = { f(u) : u in G }.
The kernel is a normal subgroup of G and the image is a subgroup of H.
Types of homomorphisms
Homomorphisms can be classified according to different criteria, among which are the relation between G and H and the nature of the mapping.
Surjective, injective and bijective homomorphisms
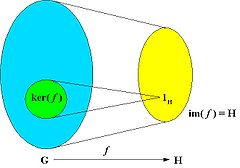
An epimorphism is a surjective homomorphism, that is, a homomorphism which is onto as a mapping. The image of the homomorphism is the whole of H, i.e. im(f) = H.
A monomorphism is an injective homomorphism, that is, a homomorphism which is one-to-one as a mapping. In this case, ker( f ) = {1G }.
If the homomorphism f is a bijection, then its inverse is also a group homomorphism, and f is called an isomorphism; the groups (G,*) and (H,#) are called isomorphic and differ only in the notation of their elements (and possibly their binary operations), while they can be regarded as identical for most practical purposes.
Homomorphisms from a group to itself (G = H)
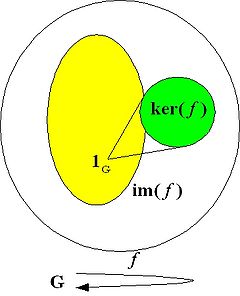
An endomorphism is a homomorphism of a group to itself: f : G → G.
A bijective (invertible) endomorphism (which is hence an isomorphism) is called an automorphism. The kernel of the automorphism is the identity of G (1G) and the image of the automorphism coincides with G. The set of all automorphisms of a group (G,*) forms itself a group, the automorphism group of G, Aut(G).