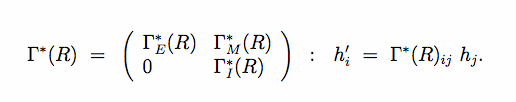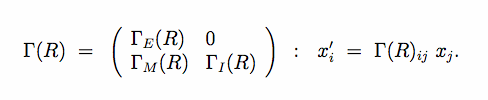Superspace point group

Groupe ponctuel de superespace (Fr). Punktgruppe des Superraums (Ge). Gruppo puntuale di superspazio (It). 超空間の点群 (Ja). Grupo puntual del superespacio (Sp).

Definition

An (m+d)-dimensional superspace group is a space group with a point group K that leaves an m-dimensional (real) subspace invariant. Therefore, K is R-reducible and its elements are pairs ([math]R_E,~R_I[/math]) of orthogonal transformations. Both [math]R_E[/math] and [math]R_I[/math] may themselves be R-reducible in turn. They form the m-dimensional point group [math]K_E[/math], and the d-dimensional point group [math]K_I[/math], respectively.

Comments

On a lattice basis the point group elements are represented by integral matrices [math]\Gamma (R)[/math]. The action of the point group on the reciprocal lattice is given by the integral matrix [math]\Gamma^*(R)[/math], which is the inverse transpose of [math]\Gamma (R)[/math].

The diffraction spots of an aperiodic crystal belong to a vector module [math]M^*[/math] that is the projection of the n-dimensional reciprocal lattice [math]\Sigma^*[/math] on the physical space. The projections of the basis vectors [math]a_{si}^*[/math] of [math]\Sigma^*[/math] are the basis vectors [math]a_{si}^*[/math] of the vector module [math]M^*[/math]. Therefore, the action of the n-dimensional point group of the superspace group on the basis of [math]M^*[/math] is

[math]R_E a_i^* ~=~ \sum_{j=1}^n \Gamma^*(R)_{ij} a_j^* ,~~(i=1,\dots,n).[/math]

For an incommensurate modulated structure, the submodule of the main reflections is invariant. As a consequence, the elements of the point group in superspace in this case is Z-reducible. There is a basis such that the point group elements are represented by the integral matrices

Both [math]\Gamma_E^*(K)[/math] and [math]\Gamma_I^*(K)[/math] are integral representations of K, as are their conjugates [math]\Gamma_E(K)[/math] and [math]\Gamma_I(K)[/math].

Points in direct space, with lattice coordinates [math]x_1,\dots,x_n[/math] transform according to

In direct space the internal space [math]V_I[/math] is left invariant, and this subspace contains a d-dimensional lattice, that is left invariant.