Group homomorphism

Homomorphisme de groupes (Fr). Gruppenhomomorphismus (Ge). Homomorfismo de grupos (Sp). Omomorfismo di gruppi (It). 準同形 (Ja).

Groups

Let G and H be two non-empty sets with binary operations * (in G) and · (in H). If * and · are associative in G and H respectively and if G and H contain an identity element and the inverse of each element in them, then (G, *) and (H, ·) are two groups.

Homomorphism between groups

A group homomorphism from (G, *) to (H, ·) is a function h : G → H that preserves the composition law, i.e. such that for all u and v in G:

h(u * v) = h(u) · h(v)

where the group operation on the left hand side of the equation is that of G and on the right hand side that of H.

The function h maps the identity element 1_G of G to the identity element 1_H of H, and it also maps inverses to inverses: h(u^-1) = h(u)^-1.

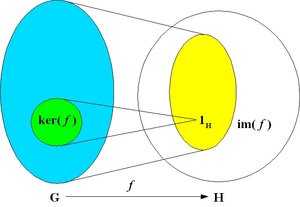
Image and kernel

Group homomorphism

The kernel of the homomorphism is the set of the elements of G that are mapped on the identity of H:

ker(h) = { u in G : h(u) = 1_H }

The image of h is the subset of elements of H that are mapped by the homomorphism h:

im(h) = { h(u) : u in G }.

The kernel is a normal subgroup and the image is a subgroup of H.

Types of homomorphisms

• If the homomorphism h is a bijection, then its inverse is also a group homomorphism, and h is called an isomorphism; the groups G and H are called isomorphic and differ only in the notation of their elements, while they are identical for all practical purposes.

• An endomorphism is a homomorphism of a group onto itself: h: G → G.
• A bijective (invertible) endomorphism (which is hence an isomorphism) is called an automorphism. The set of all automorphisms of a group G forms itself a group, the automorphism group of G, Aut(G).
• An epimorphism is a surjective homomorphism, that is, a homomorphism which is onto as a function. The image of the homomorphism spans the whole set H: in this case, img(h) = H
• A monomorphism is an injective homomorphism, that is, a homomorphism which is one-to-one as a function. In this case, ker(h) = {1_G }.