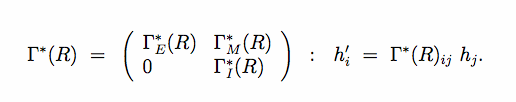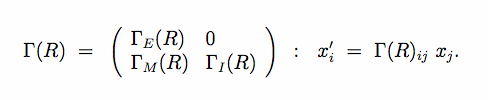Difference between revisions of "Superspace point group"
From Online Dictionary of Crystallography
TedJanssen (talk | contribs) |
BrianMcMahon (talk | contribs) m |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
<Font color="blue">Groupe ponctuel de superespace</font> (Fr.) | <Font color="blue">Groupe ponctuel de superespace</font> (Fr.) | ||
| − | + | == Definition == | |
An (''m+d'')-dimensional superspace group is a space group with a point group ''K'' that leaves | An (''m+d'')-dimensional superspace group is a space group with a point group ''K'' that leaves | ||
| Line 9: | Line 7: | ||
pairs (<math>R_E,~R_I</math>) of orthogobal transformations. Both <math>R_E</math> and <math>R_I</math> may themselves be R-reducible in turn. They form the ''m''-dimensional point group <math>K_E</math>, and the ''d''-dimensional point group <math>K_I</math>, respectively. | pairs (<math>R_E,~R_I</math>) of orthogobal transformations. Both <math>R_E</math> and <math>R_I</math> may themselves be R-reducible in turn. They form the ''m''-dimensional point group <math>K_E</math>, and the ''d''-dimensional point group <math>K_I</math>, respectively. | ||
| − | + | == Comments == | |
On a lattice basis the point group elements are represented by integral matrices <math>\Gamma (R)</math>. | On a lattice basis the point group elements are represented by integral matrices <math>\Gamma (R)</math>. | ||
| Line 20: | Line 18: | ||
<math>R_E a_i^* ~=~ \sum_{j=1}^n \Gamma^*(R)_{ij} a_j^* ,~~(i=1,\dots,n).</math> | <math>R_E a_i^* ~=~ \sum_{j=1}^n \Gamma^*(R)_{ij} a_j^* ,~~(i=1,\dots,n).</math> | ||
| − | |||
For an [[incommensurate modulated structure]], the submodule of the main reflections is invariant. As a consequence, the elements of the point group in superspace in this case is Z-reducible. There is a basis | For an [[incommensurate modulated structure]], the submodule of the main reflections is invariant. As a consequence, the elements of the point group in superspace in this case is Z-reducible. There is a basis | ||
Revision as of 11:29, 8 February 2012
Groupe ponctuel de superespace (Fr.)
Definition
An (m+d)-dimensional superspace group is a space group with a point group K that leaves an m-dimensional (real) subspace invariant. Therefore, K is R-reducible and its elements are pairs ([math]R_E,~R_I[/math]) of orthogobal transformations. Both [math]R_E[/math] and [math]R_I[/math] may themselves be R-reducible in turn. They form the m-dimensional point group [math]K_E[/math], and the d-dimensional point group [math]K_I[/math], respectively.
Comments
On a lattice basis the point group elements are represented by integral matrices [math]\Gamma (R)[/math]. The action of the point group on the reciprocal lattice is given by the integral matrix [math]\Gamma^*(R)[/math], which is the inverse transpose of [math]\Gamma (R)[/math].
The diffraction spots of an aperiodic crystal belong to a vector module [math]M^*[/math] that is the projection of the n-dimensional reciprocal lattice [math]\Sigma^*[/math] on the physical space. The projections of the basis vectors [math]a_{si}^*[/math] of [math]\Sigma^*[/math] are the basis vectors [math]a_{si}^*[/math] of the vector module [math]M^*[/math]. Therefore, the action of the n-dimensional point group of the superspace group on the basis of [math]M^*[/math] is
[math]R_E a_i^* ~=~ \sum_{j=1}^n \Gamma^*(R)_{ij} a_j^* ,~~(i=1,\dots,n).[/math]
For an incommensurate modulated structure, the submodule of the main reflections is invariant. As a consequence, the elements of the point group in superspace in this case is Z-reducible. There is a basis such that the point group elements are represented by the integral matrices
Both [math]\Gamma_E^*(K)[/math] and [math]\Gamma_I^*(K)[/math] are integral representations of K, as are their conjugates [math]\Gamma_E(K)[/math] and [math]\Gamma_I(K)[/math].
Points in direct space, with lattice coordinates [math]x_1,\dots,x_n[/math] transform according to
In direct space the internal space [math]V_I[/math] is left invariant, and this subspace contains a d-dimensional lattice, that is left invariant.