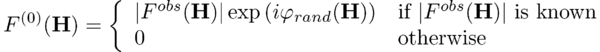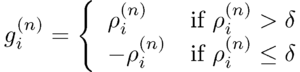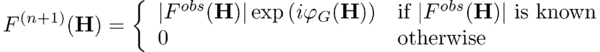Difference between revisions of "Charge flipping"
From Online Dictionary of Crystallography
BrianMcMahon (talk | contribs) m (Style edits to align with printed edition) |
|||
| (6 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
== Definition == | == Definition == | ||
| − | Charge flipping is a structure solution method from the class of [[dual-space phase retrieval algorithms|dual-space algorithms]]. The key component of the charge flipping algorithm is the charge flipping operation. In this operation, all scattering density pixels with density lower than a small positive threshold delta are multiplied by -1 (flipped). In the classical charge flipping algorithm, this direct-space modification is combined with simple resubstitution of structure-factor amplitudes by experimental values, but other modifications and iteration schemes have been proposed and successfully used. | + | Charge flipping is a structure solution method from the class of [[dual-space phase retrieval algorithms|dual-space algorithms]]. The key component of the charge flipping algorithm is the charge flipping operation. In this operation, all scattering density pixels with density lower than a small positive threshold δ are multiplied by -1 (flipped). In the classical charge flipping algorithm, this direct-space modification is combined with simple resubstitution of structure-factor amplitudes by experimental values, but other modifications and iteration schemes have been proposed and successfully used. |
Given a trial scattering density <math>\rho</math> sampled on a regular grid, and a set of measured structure-factor amplitudes <math>F^{obs}(\mathbf{H})</math>, the basic charge flipping algorithm follows this scheme: | Given a trial scattering density <math>\rho</math> sampled on a regular grid, and a set of measured structure-factor amplitudes <math>F^{obs}(\mathbf{H})</math>, the basic charge flipping algorithm follows this scheme: | ||
| Line 13: | Line 13: | ||
# The density <math>\rho^{(n)}</math> is calculated by inverse Fourier transform of <math>F^{(n)}</math>. | # The density <math>\rho^{(n)}</math> is calculated by inverse Fourier transform of <math>F^{(n)}</math>. | ||
| − | # The modified density <math>g^{(n)}</math> is obtained by flipping the density of all pixels with density values below a certain positive threshold <math>\delta</math> and keeping the rest of the pixels unchanged: | + | # The modified density <math>g^{(n)}</math> is obtained by flipping the density of all pixels with density values below a certain positive threshold <math>\delta</math> and keeping the rest of the pixels unchanged:[[Image:CF_2.png|300px|center]]<br> |
| − | [[Image:CF_2.png|300px|center]]<br> | ||
#Temporary structure factors <math>G^{(n)}(\mathbf{H})=|G^{(n)}(\mathbf{H})|\exp{(i\varphi_{G}(\mathbf{H}))}</math> are calculated by Fourier transform of <math>g^{(n)}</math>.<br> | #Temporary structure factors <math>G^{(n)}(\mathbf{H})=|G^{(n)}(\mathbf{H})|\exp{(i\varphi_{G}(\mathbf{H}))}</math> are calculated by Fourier transform of <math>g^{(n)}</math>.<br> | ||
| − | #New structure factors <math>F^{(n+1)}</math> are obtained by combining the experimental amplitudes with the phases <math>\varphi_{G}</math> and setting all non-measured structure factors to zero: | + | #New structure factors <math>F^{(n+1)}</math> are obtained by combining the experimental amplitudes with the phases <math>\varphi_{G}</math> and setting all non-measured structure factors to zero:<br>[[Image:CF_3.png|600px|center]]<br> |
| − | + | These modified structure factors then enter the next cycle of iteration. | |
| − | + | ==See also== | |
| + | *[[Dual-space phase retrieval algorithms]] | ||
| + | |||
| + | [[Category: Structure determination]] | ||
Latest revision as of 10:35, 13 May 2017
Definition
Charge flipping is a structure solution method from the class of dual-space algorithms. The key component of the charge flipping algorithm is the charge flipping operation. In this operation, all scattering density pixels with density lower than a small positive threshold δ are multiplied by -1 (flipped). In the classical charge flipping algorithm, this direct-space modification is combined with simple resubstitution of structure-factor amplitudes by experimental values, but other modifications and iteration schemes have been proposed and successfully used.
Given a trial scattering density [math]\rho[/math] sampled on a regular grid, and a set of measured structure-factor amplitudes [math]F^{obs}(\mathbf{H})[/math], the basic charge flipping algorithm follows this scheme:
First, the algorithm is initiated in the zeroth cycle by assigning random starting phases [math]\varphi_{rand}(\mathbf{H})[/math] to all experimental amplitudes and making all unobserved amplitudes equal to zero:
The iteration cycle then proceeds as follows:
- The density [math]\rho^{(n)}[/math] is calculated by inverse Fourier transform of [math]F^{(n)}[/math].
- The modified density [math]g^{(n)}[/math] is obtained by flipping the density of all pixels with density values below a certain positive threshold [math]\delta[/math] and keeping the rest of the pixels unchanged:
- Temporary structure factors [math]G^{(n)}(\mathbf{H})=|G^{(n)}(\mathbf{H})|\exp{(i\varphi_{G}(\mathbf{H}))}[/math] are calculated by Fourier transform of [math]g^{(n)}[/math].
- New structure factors [math]F^{(n+1)}[/math] are obtained by combining the experimental amplitudes with the phases [math]\varphi_{G}[/math] and setting all non-measured structure factors to zero:
These modified structure factors then enter the next cycle of iteration.