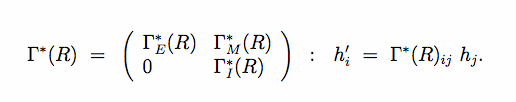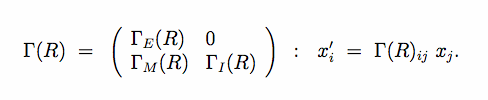Difference between revisions of "Superspace point group"
From Online Dictionary of Crystallography
TedJanssen (talk | contribs) |
BrianMcMahon (talk | contribs) (Tidied translations and added German and Spanish (U. Mueller)) |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <font color="blue">Groupe ponctuel de superespace</font> (''Fr''). <font color="red">Punktgruppe des Superraums</font> (''Ge''). <font color="black">Gruppo puntuale di superspazio</font> (''It''). <font color="purple">超空間の点群</font> (''Ja''). <font color="green">Grupo puntual del superespacio</font> (''Sp''). | |
| − | |||
| − | + | == Definition == | |
An (''m+d'')-dimensional superspace group is a space group with a point group ''K'' that leaves | An (''m+d'')-dimensional superspace group is a space group with a point group ''K'' that leaves | ||
an ''m''-dimensional (real) subspace invariant. Therefore, ''K'' is R-reducible and its elements are | an ''m''-dimensional (real) subspace invariant. Therefore, ''K'' is R-reducible and its elements are | ||
| − | pairs (<math>R_E,~R_I</math>) of | + | pairs (<math>R_E,~R_I</math>) of orthogonal transformations. Both <math>R_E</math> and <math>R_I</math> may themselves be R-reducible in turn. They form the ''m''-dimensional point group <math>K_E</math>, and the ''d''-dimensional point group <math>K_I</math>, respectively. |
| − | + | == Comments == | |
On a lattice basis the point group elements are represented by integral matrices <math>\Gamma (R)</math>. | On a lattice basis the point group elements are represented by integral matrices <math>\Gamma (R)</math>. | ||
| Line 17: | Line 16: | ||
projection of the ''n''-dimensional reciprocal lattice <math>\Sigma^*</math> on the physical space. The projections | projection of the ''n''-dimensional reciprocal lattice <math>\Sigma^*</math> on the physical space. The projections | ||
of the basis vectors <math>a_{si}^*</math> of <math>\Sigma^*</math> are the basis vectors <math>a_{si}^*</math> of the vector module <math>M^*</math>. Therefore, | of the basis vectors <math>a_{si}^*</math> of <math>\Sigma^*</math> are the basis vectors <math>a_{si}^*</math> of the vector module <math>M^*</math>. Therefore, | ||
| − | the action of the n-dimensional point group of the superspace group on the basis of <math>M^*</math> is | + | the action of the ''n''-dimensional point group of the superspace group on the basis of <math>M^*</math> is |
<math>R_E a_i^* ~=~ \sum_{j=1}^n \Gamma^*(R)_{ij} a_j^* ,~~(i=1,\dots,n).</math> | <math>R_E a_i^* ~=~ \sum_{j=1}^n \Gamma^*(R)_{ij} a_j^* ,~~(i=1,\dots,n).</math> | ||
| − | |||
For an [[incommensurate modulated structure]], the submodule of the main reflections is invariant. As a consequence, the elements of the point group in superspace in this case is Z-reducible. There is a basis | For an [[incommensurate modulated structure]], the submodule of the main reflections is invariant. As a consequence, the elements of the point group in superspace in this case is Z-reducible. There is a basis | ||
| Line 35: | Line 33: | ||
In direct space the internal space <math>V_I</math> is left invariant, and this subspace contains a ''d''-dimensional lattice, that is left invariant. | In direct space the internal space <math>V_I</math> is left invariant, and this subspace contains a ''d''-dimensional lattice, that is left invariant. | ||
| + | |||
| + | [[Category: Fundamental crystallography]] | ||
Latest revision as of 09:17, 20 November 2017
Groupe ponctuel de superespace (Fr). Punktgruppe des Superraums (Ge). Gruppo puntuale di superspazio (It). 超空間の点群 (Ja). Grupo puntual del superespacio (Sp).
Definition
An (m+d)-dimensional superspace group is a space group with a point group K that leaves an m-dimensional (real) subspace invariant. Therefore, K is R-reducible and its elements are pairs ([math]R_E,~R_I[/math]) of orthogonal transformations. Both [math]R_E[/math] and [math]R_I[/math] may themselves be R-reducible in turn. They form the m-dimensional point group [math]K_E[/math], and the d-dimensional point group [math]K_I[/math], respectively.
Comments
On a lattice basis the point group elements are represented by integral matrices [math]\Gamma (R)[/math]. The action of the point group on the reciprocal lattice is given by the integral matrix [math]\Gamma^*(R)[/math], which is the inverse transpose of [math]\Gamma (R)[/math].
The diffraction spots of an aperiodic crystal belong to a vector module [math]M^*[/math] that is the projection of the n-dimensional reciprocal lattice [math]\Sigma^*[/math] on the physical space. The projections of the basis vectors [math]a_{si}^*[/math] of [math]\Sigma^*[/math] are the basis vectors [math]a_{si}^*[/math] of the vector module [math]M^*[/math]. Therefore, the action of the n-dimensional point group of the superspace group on the basis of [math]M^*[/math] is
[math]R_E a_i^* ~=~ \sum_{j=1}^n \Gamma^*(R)_{ij} a_j^* ,~~(i=1,\dots,n).[/math]
For an incommensurate modulated structure, the submodule of the main reflections is invariant. As a consequence, the elements of the point group in superspace in this case is Z-reducible. There is a basis such that the point group elements are represented by the integral matrices
Both [math]\Gamma_E^*(K)[/math] and [math]\Gamma_I^*(K)[/math] are integral representations of K, as are their conjugates [math]\Gamma_E(K)[/math] and [math]\Gamma_I(K)[/math].
Points in direct space, with lattice coordinates [math]x_1,\dots,x_n[/math] transform according to
In direct space the internal space [math]V_I[/math] is left invariant, and this subspace contains a d-dimensional lattice, that is left invariant.