Group homomorphism

Homomorphisme de groupes (Fr). Gruppenhomomorphismus (Ge). Homomorfismo de grupos (Sp). Omomorfismo di gruppi (It). 準同形 (Ja).

Groups

Let G and H be two non-empty sets with binary operations * (in G) and # (in H). If * and # are associative in G and H respectively and if G and H contain an identity element and the inverse of each element in them, then (G, *) and (H, #) are two groups.

Homomorphism between groups

A group homomorphism from (G, *) to (H, #) is a function f : G → H that preserves the composition law, i.e. such that for all u and v in G:

f(u * v) = f(u) # f(v).

The function f maps the identity element 1_G of G to the identity element 1_H of H, and it also maps inverses to inverses: f(u^-1) = f(u)^-1.

Image and kernel

Group homomorphism. The kernel of the homomorphism, ker( f ) is the set of elements of G that are mapped on the identity element of H. The image of the homomorphism, im( f ), is the set of elements of H with one or more corresponding element in G. im( f ) is not required to span the whole H

.

The kernel of the homomorphism is the set of the elements of G that are mapped on the identity of H:

ker( f ) = { u in G : f(u) = 1_H }

The image of the homomorphism is the subset of elements of H that are mapped by the homomorphism f:

im( f ) = { f(u) : u in G }.

The kernel is a normal subgroup and the image is a subgroup of H.

Types of homomorphisms

An epimorphism is a surjective homomorphism, i.e. a homomorphism where the image spans the whole codomain

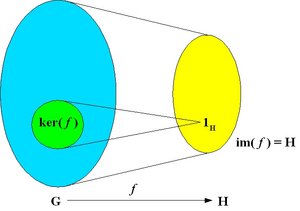
• An epimorphism is a surjective homomorphism, that is, a homomorphism which is onto as a function. The image of the homomorphism spans the whole set H: in this case, img(f) = H
• A monomorphism is an injective homomorphism, that is, a homomorphism which is one-to-one as a function. In this case, ker( f ) = {1_G }.
• If the homomorphism f is a bijection, then its inverse is also a group homomorphism, and f is called an isomorphism; the groups G and H are called isomorphic and differ only in the notation of their elements, while they are identical for all practical purposes.
• An endomorphism is a homomorphism of a group onto itself: f: G → G.
• A bijective (invertible) endomorphism (which is hence an isomorphism) is called an automorphism. The set of all automorphisms of a group G forms itself a group, the automorphism group of G, Aut(G).