Group homomorphism

Homomorphisme de groupes (Fr). Gruppenhomomorphismus (Ge). Homomorfismo de grupos (Sp). Omomorfismo di gruppi (It). 準同形 (Ja).

Homomorphism between groups

A group homomorphism from a group (G, *) to a group (H, #) is a mapping f : G → H that preserves the composition law, i.e. for all u and v in G one has:

f(u * v) = f(u) # f(v).

A homomorphism f maps the identity element 1_G of G to the identity element 1_H of H, and it also maps inverses to inverses: f(u^-1) = f(u)^-1.

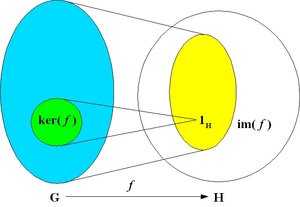
Kernel and image

Group homomorphism. The kernel of the homomorphism, ker( f ) is the set of elements of G that are mapped to the identity element of H. The image of the homomorphism, im( f ), is the set of elements of H to which at least one element of G is mapped. im( f ) is not required to be the whole of H

.

The kernel of the homomorphism f is the set of elements of G that are mapped to the identity of H:

ker( f ) = { u in G : f(u) = 1_H }

The image of the homomorphism f is the subset of elements of H to which at least one element of G is mapped by f:

im( f ) = { f(u) : u in G }.

The kernel is a normal subgroup of G and the image is a subgroup of H.

Types of homomorphisms

Homomorphisms can be classified according to different criteria, among which the relation between G and H and the nature of the mapping.

Surjective, injective and bijective homomorphisms

An epimorphism is a surjective homomorphism, i.e. a homomorphism such that the image is the entire codomain

.

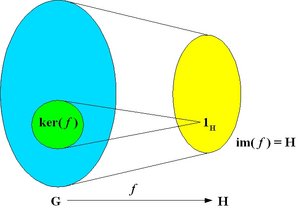
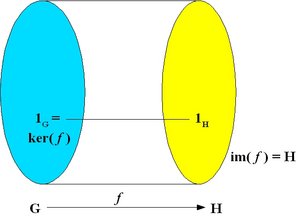
An epimorphism is a surjective homomorphism, that is, a homomorphism which is onto as a mapping. The image of the homomorphism is the whole of H, i.e. im( f ) = H

A monomorphism is an injective homomorphism, i.e. a homomorphism where different elements of G are mapped to different elements of H

.

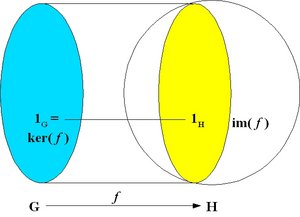
A monomorphism is an injective homomorphism, that is, a homomorphism which is one-to-one as a mapping. In this case, ker( f ) = {1_G }.

An isomorphism is a bijective homomorphism, i.e. it is a one-to-one correspondence between the elements of G and those of H. Isomorphic groups (G,*) and (H,#) differ only in the notation of their elements and binary operations

.

If the homomorphism f is a bijection, then its inverse is also a group homomorphism, and f is called an isomorphism; the groups (G,*) and (H,#) are called isomorphic and differ only in the notation of their elements (and possibly their binary operations), while they can be regarded as identical for most practical purposes.

Homomorphisms from a group to itself (G = H)

An endomorphism is homomorphism of G to itself

.

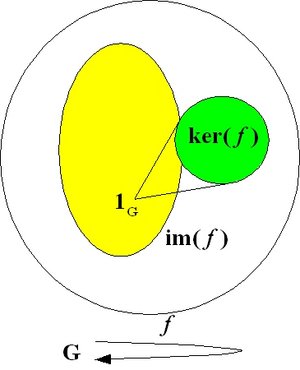
An endomorphism is a homomorphism of a group to itself: f: G → G.

A bijective (invertible) endomorphism (which is hence an isomorphism) is called an automorphism. The kernel of the automorphism is the identity of G (1_G) and the image of the automorphism coincides with G. The set of all automorphisms of a group (G,*) forms itself a group, the automorphism group of G, Aut(G).