Difference between revisions of "Group homomorphism"
From Online Dictionary of Crystallography
(→Types of homomorphisms: More details and figures) |
(→Kernel and image: Bold) |
||
| Line 15: | Line 15: | ||
== Kernel and image== | == Kernel and image== | ||
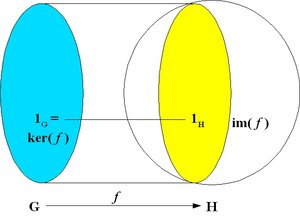
| − | [[Image:Homomorphism.jpg|thumb|300px|Group homomorphism. The kernel of the homomorphism, ker( ''f'' ) is the set of elements of ''G'' that are mapped on the identity element of ''H''. The image of the homomorphism, im( ''f'' ), is the set of elements of ''H'' with one or more corresponding element in ''G''. im( ''f'' ) is not required to span the whole ''H'']]. | + | [[Image:Homomorphism.jpg|thumb|300px|'''Group homomorphism'''. The kernel of the homomorphism, ker( ''f'' ) is the set of elements of ''G'' that are mapped on the identity element of ''H''. The image of the homomorphism, im( ''f'' ), is the set of elements of ''H'' with one or more corresponding element in ''G''. im( ''f'' ) is not required to span the whole ''H'']]. |
The ''kernel'' of the homomorphism is the set of the elements of ''G'' that are [[mapping|mapped]] on the identity of ''H'': | The ''kernel'' of the homomorphism is the set of the elements of ''G'' that are [[mapping|mapped]] on the identity of ''H'': | ||
<div align="center"> | <div align="center"> | ||
Revision as of 14:36, 19 March 2009
Homomorphisme de groupes (Fr). Gruppenhomomorphismus (Ge). Homomorfismo de grupos (Sp). Omomorfismo di gruppi (It). 準同形 (Ja).
Contents
[hide]Groups
Let G and H be two non-empty sets with binary operations * (in G) and # (in H). If * and # are associative in G and H respectively and if G and H contain an identity element and the inverse of each element in them, then (G, *) and (H, #) are two groups.
Homomorphism between groups
A group homomorphism from (G, *) to (H, #) is a function f : G → H that preserves the composition law, i.e. such that for all u and v in G:
f(u * v) = f(u) # f(v).
The function f maps the identity element 1G of G to the identity element 1H of H, and it also maps inverses to inverses: f(u-1) = f(u)-1.
Kernel and image
The kernel of the homomorphism is the set of the elements of G that are mapped on the identity of H:
ker( f ) = { u in G : f(u) = 1H }
The image of the homomorphism is the subset of elements of H that are mapped by the homomorphism f:
im( f ) = { f(u) : u in G }.
The kernel is a normal subgroup and the image is a subgroup of H.
Types of homomorphisms
Homomorphisms can be classified according to different criteria, among which the relation between G and H and the nature of the mapping.
Homomorphisms mapping elements of different sets (G ≠ H)
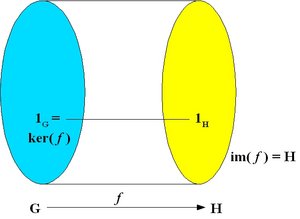
An epimorphism is a surjective homomorphism, that is, a homomorphism which is onto as a function. The image of the homomorphism spans the whole set H: in this case, img( f ) = H
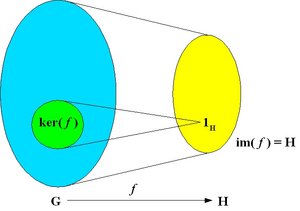
A monomorphism is an injective homomorphism, that is, a homomorphism which is one-to-one as a function. In this case, ker( f ) = {1G }.
If the homomorphism f is a bijection, then its inverse is also a group homomorphism, and f is called an isomorphism; the groups (G,*) and (H,#) are called isomorphic and differ only in the notation of their elements, while they are identical for all practical purposes.
Homomorphisms mapping elements of the same set (G = H)
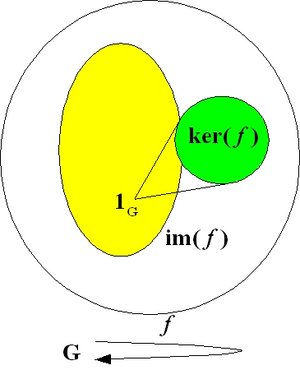
.An endomorphism is a homomorphism of a group onto itself: f: G → G.
A bijective (invertible) endomorphism (which is hence an isomorphism) is called an automorphism. The kernel of the automorphism is the identity of G (1G) and the image of the automorphism coincides with G. The set of all automorphisms of a group (G,*) forms itself a group, the automorphism group of G, Aut(G).