Difference between revisions of "Wigner-Seitz cell"
From Online Dictionary of Crystallography
m (→See also: ITA 6th edition) |
BrianMcMahon (talk | contribs) m (Style edits to align with printed edition) |
||
| Line 1: | Line 1: | ||
| − | <Font color="blue"> Maille de Wigner-Seitz </Font>(''Fr''). <Font color="red"> Wigner-Seitz Zell </Font>(''Ge''). <Font color="green"> Celda de Wigner-Seitz</Font> (''Sp'').<Font color="black"> Cella di Wigner-Seitz </Font>(''It'') | + | <Font color="blue"> Maille de Wigner-Seitz </Font>(''Fr''). <Font color="red"> Wigner-Seitz Zell </Font>(''Ge''). <Font color="green"> Celda de Wigner-Seitz</Font> (''Sp'').<Font color="black"> Cella di Wigner-Seitz </Font>(''It''). |
== Definition == | == Definition == | ||
| Line 5: | Line 5: | ||
[[Image:W-S-1.gif|right]] | [[Image:W-S-1.gif|right]] | ||
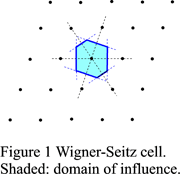
| − | The Wigner-Seitz cell is | + | The Wigner-Seitz cell is a polyhedron obtained by connecting a lattice point ''P'' to all other lattice points and drawing the planes perpendicular to these connecting lines and passing through their midpoints (Fig. 1). The polyhedron enclosed by these planes is the Wigner-Seitz cell. This construction is called the Dirichlet construction. The cell thus obtained is a primitive cell and it is possible to fill up the whole space by translation of that cell. |
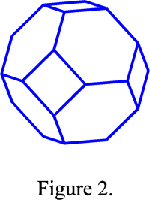
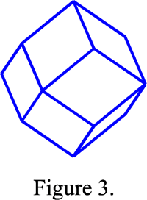
| − | The Wigner-Seitz cell of a body-centred cubic lattice ''I'' is a cuboctahedron ( | + | The Wigner-Seitz cell of a body-centred cubic lattice ''I'' is a cuboctahedron (Fig. 2) and the Wigner-Seitz cell of a face-centred cubic lattice ''F'' is a rhomb-dodecahedron (Fig. 3). In reciprocal space this cell is the first Brillouin zone. Since the reciprocal lattice of a body-centred lattice is a face-centred lattice and reciprocally, the first [[Brillouin_zones|Brillouin zone]] of a body-centred cubic lattice is a rhomb-dodecahedron and that of a face-centred cubic lattice is a cuboctahedron. |
<center> | <center> | ||
| Line 14: | Line 14: | ||
</center> | </center> | ||
| − | The inside of the Wigner-Seitz cell has been called [[domain of influence]] by Delaunay (1933). It is also called Dirichlet domain or [[Voronoi domain]]. The domain of influence of lattice point ''P'' thus consists of all points ''Q'' in space that are closer to this lattice point than to any other lattice point or at most equidistant to it (such that '''OP''' ≤ |'''t''' - '''OP'''| for any vector '''t''' ∈ ''L''). | + | The inside of the Wigner-Seitz cell has been called the [[domain of influence]] by Delaunay (1933). It is also called the Dirichlet domain or [[Voronoi domain]]. The domain of influence of lattice point ''P'' thus consists of all points ''Q'' in space that are closer to this lattice point than to any other lattice point or at most equidistant to it (such that '''OP''' ≤ |'''t''' - '''OP'''| for any vector '''t''' ∈ ''L''). |
== See also == | == See also == | ||
| − | * | + | *Chapter 3.1.1.4 of ''International Tables for Crystallography, Volume A'', 6th edition |
| − | * | + | *Chapter 1.5 of ''International Tables for Crystallography, Volume B'' |
| − | * | + | *Chapters 1.2 and 2.2 of ''International Tables for Crystallography, Volume D'' |
[[Category:Fundamental crystallography]] | [[Category:Fundamental crystallography]] | ||
Revision as of 18:21, 17 May 2017
Maille de Wigner-Seitz (Fr). Wigner-Seitz Zell (Ge). Celda de Wigner-Seitz (Sp). Cella di Wigner-Seitz (It).
Definition
The Wigner-Seitz cell is a polyhedron obtained by connecting a lattice point P to all other lattice points and drawing the planes perpendicular to these connecting lines and passing through their midpoints (Fig. 1). The polyhedron enclosed by these planes is the Wigner-Seitz cell. This construction is called the Dirichlet construction. The cell thus obtained is a primitive cell and it is possible to fill up the whole space by translation of that cell.
The Wigner-Seitz cell of a body-centred cubic lattice I is a cuboctahedron (Fig. 2) and the Wigner-Seitz cell of a face-centred cubic lattice F is a rhomb-dodecahedron (Fig. 3). In reciprocal space this cell is the first Brillouin zone. Since the reciprocal lattice of a body-centred lattice is a face-centred lattice and reciprocally, the first Brillouin zone of a body-centred cubic lattice is a rhomb-dodecahedron and that of a face-centred cubic lattice is a cuboctahedron.
The inside of the Wigner-Seitz cell has been called the domain of influence by Delaunay (1933). It is also called the Dirichlet domain or Voronoi domain. The domain of influence of lattice point P thus consists of all points Q in space that are closer to this lattice point than to any other lattice point or at most equidistant to it (such that OP ≤ |t - OP| for any vector t ∈ L).
See also
- Chapter 3.1.1.4 of International Tables for Crystallography, Volume A, 6th edition
- Chapter 1.5 of International Tables for Crystallography, Volume B
- Chapters 1.2 and 2.2 of International Tables for Crystallography, Volume D