Wigner-Seitz cell
From Online Dictionary of Crystallography
Revision as of 14:50, 20 November 2017 by BrianMcMahon (talk | contribs) (Tidied translations and corrected German (U. Mueller))
Synonym: Voronoi domain
Maille de Wigner-Seitz (Fr). Wigner-Seitz-Zelle, Wirkungsbereich (Ge). Cella di Wigner-Seitz (It). Celda de Wigner-Seitz (Sp).
Definition
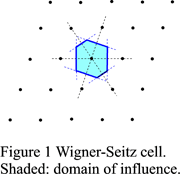
The Wigner-Seitz cell is a polyhedron obtained by connecting a lattice point P to all other lattice points and drawing the planes perpendicular to these connecting lines and passing through their midpoints (Fig. 1). The polyhedron enclosed by these planes is the Wigner-Seitz cell. This construction is called the Dirichlet construction. The cell thus obtained is a primitive cell and it is possible to fill up the whole space by translation of that cell.
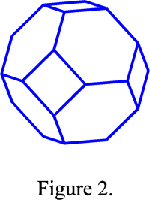
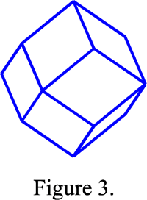
The Wigner-Seitz cell of a body-centred cubic lattice I is a cuboctahedron (Fig. 2) and the Wigner-Seitz cell of a face-centred cubic lattice F is a rhomb-dodecahedron (Fig. 3). In reciprocal space this cell is the first Brillouin zone. Since the reciprocal lattice of a body-centred lattice is a face-centred lattice and reciprocally, the first Brillouin zone of a body-centred cubic lattice is a rhomb-dodecahedron and that of a face-centred cubic lattice is a cuboctahedron.
The inside of the Wigner-Seitz cell has been called the domain of influence by Delaunay (1933). It is also called the Dirichlet domain or Voronoi domain. The domain of influence of lattice point P thus consists of all points Q in space that are closer to this lattice point than to any other lattice point or at most equidistant to it (such that OP ≤ |t - OP| for any vector t ∈ L).
See also
- Chapter 3.1.1.4 of International Tables for Crystallography, Volume A, 6th edition
- Chapter 1.5 of International Tables for Crystallography, Volume B
- Chapters 1.2 and 2.2 of International Tables for Crystallography, Volume D